Composizione concorrente
Cos'è la composizione concorrente
La composizione concorrente di due linguaggio L1 di E2 e L2 di E2 è il linguaggio L1||L2 composto dalle parole di L1 che sono proiezioni su E1 e dalle parole di L2 che sono proiezioni su E2. $$ L_1||L_2 = \{ w \in E \: : \: w↑ E_1 \in L_1, w↑ E_2 \in L_2 \} $$ con $$ E = (E_1∪E_2) $$
Un esempio pratico
Dati due insiemi di simboli E1 e E2
$$ E_1 = \{ a,b \} $$
$$ E_2 = \{ b,c \} $$
Ho anche due linguaggi determinati dalle seguenti regole
$$ L_1 = \{ ab^n| n \ge 0 \} $$
$$ L_2 = \{ cbc^nb| n \ge 0 \} $$
Esempio. Il linguaggio L1 è composto dalle seguenti parole $$ L_1 = \{ ab, abb, abbb, ... \} $$ mentre il linguaggio L2 è composto dalle seguenti parole $$ L_2 = \{ cbcb, cbccb, cbcccb, ... \} $$
Per calcolare la composizione concorrente determino l'insieme unione E
$$ E = E_1 ∪ E_2 = \{ a,b,c \} $$
Esempio. L'insieme E è composto dall'unione dei simboli degli alfabeti E1 e E2. Il linguaggio generato L da E è un insieme di parole di qualsiasi lunghezza composte dai simboli a,b,c $$ L = \{ abc, acb, cab, abcba, ... \} $$
La composizione concorrente dei linguaggi L1||L2 è l'insieme delle parole w le cui proiezioni sugli alfabeti E1 ed E2 appartengono rispettivamente al linguaggio L1 e L2.
$$ L_1||L_2 = \{ w \in E \: : \: w↑ E_1 \in L_1, w↑ E_2 \in L_2 \} $$
Ecco l'analisi di alcune parole w generate da E
| w | w↑E1 | w↑E1∈L1 | w↑E2 | w↑E2∈L2 | w∈L1||L2 |
|---|---|---|---|---|---|
| abc | ab | si | bc | no | no |
| ab | ab | si | b | no | no |
| abca | aba | no | bc | no | no |
| abbc | abb | si | bbc | no | no |
| abcb | abb | si | bcb | no | no |
| acbcb | abb | si | cbcb | si | si |
| ... |
Nota. Nell'esempio precedente soltanto la parola w=acbcb appartiene alla composizione concorrente L1||L2 perché la la proiezione w↑E1 appartiene a L1 e la proiezione w↑E2 appartiene a L2. Le altre parole, invece, non rispettano entrambe le condizioni.
Spiegazione
Devo trovare le proiezioni delle parole w generate dall'alfabeto E=E1∪E2 incluse sia nel linguaggio L1 che L2.
$$ w↑E_1 \in L_1 \\ w↑E_2 \in L_2 $$
Le proiezioni delle parole w su E1 sono $$ w↑E_1 = \{ a,b,ab,ba,abb,aba, ... \} $$ mentre le proiezioni delle parole w su E2 sono $$ w↑E_2 = \{ cb, bc, cbc, cbb, bcb, ... \} $$
Queste parole appartengono al linguaggio generato.
Di queste parole devo considerare soltanto quelle che rispettano le regole dei rispettivi linguaggi L1 e L2 ossia il linguaggio accettato.
$$ L_1 = \{ ab^n| n \ge 0 \} $$
$$ L_2 = \{ cbc^nb| n \ge 0 \} $$
Le proiezioni delle parole w su E1 che appartengono a L1 sono $$ w↑E_1 = \{ ab,abb,abbb, ... \} = \{ ab^n \} $$ mentre le proiezioni delle parole w su E2 che appartengono a L2 sono $$ w↑E_2 = \{ cbcb, cbccb, cbcccb,... \} = \{ cbc^nb \} $$
L'intersezione di questi due insiemi individua le parole presenti sia in L1 che in L2.
$$ w↑E_1⋂w↑E_2=\{ acbc^nb, cabc^nb \} $$
Sono le parole della composizione concorrente del linguaggio
$$ L_1||L_2= \{ acbc^nb | n \ge 0 \} ∪ \{ cabc^nb | n \ge 0 \} $$
Nota. Le proiezioni della parola acbcnb appartengono a entrambi i linguaggi. $$ acbc^nb↑E_1 = ab^n \in L_1 \\ acbc^nb↑E_2 = cbc^nb \in L_2 $$ Le proiezioni della parola cabcnb appartengono a entrambi i linguaggi. $$ cabc^nb↑E_1 = ab^n \in L_1 \\ cabc^nb↑E_2 = cbc^nb \in L_2 $$
La composizione concorrente degli automi
Per determinare la composizione concorrente di due automi a stati finiti, posso unire le reti A e B in un'unica rete.
In questo modo ottengo un terzo automa C.
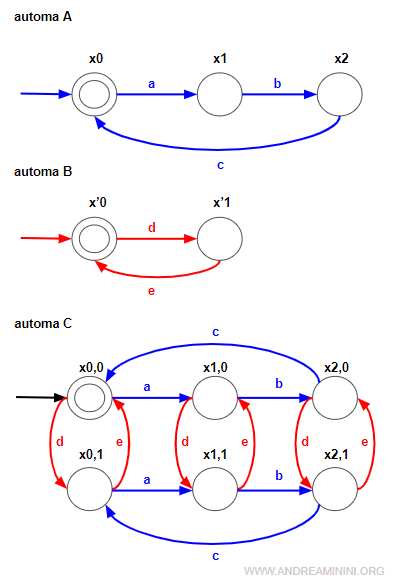
Nota. Ogni nodo della rete A^B è composto da due indici xi,j. Il primo indice "i" indica lo stato dell'automa A quando si verifica una sequenza di eventi w. Il secondo indice "j" indica lo stato dell'automa B per la stessa sequenza di eventi w.
L'insieme degli eventi EC dell'automa C è uguale all'unione di EA e EB.
$$ E_C = E_A ∪ E_B = \{ a,b,c \} ∪ \{ d,e \} = \{ a,b,c,d,e \} $$
Il linguaggio accettato dell'automa C è uguale alla composizione concorrente due due automi A e B.
$$ L_m(C) = A \: || \: B $$
L'automa C accetta sia le sequenze di eventi (ε,a,ab,abc) dell'automa A e sia le sequenze di eventi (ε,d,de) dell'automa B.
Inoltre, l'automa C accetta anche altre combinazioni w che proiettate sui rispettivi insiemi degli aventi EA e EB appartengono sia ad A che a B.
Esempio. La sequenza w="ade" è una parola accettata dall'automa C pur non appartenendo ad A e B. La proiezione w↑EA="a"∈A è accettata dall'automa A. La proiezione w↑EB="de"∈A è accettata dall'automa B. Quindi, la sequenza w="ade" appartiene alla composizione concorrente A || B.
E così via.
