La consistenza strutturale della rete
Una rete N è strutturalmente consistente se esiste una marcatura iniziale M0 che genera una sequenza ripetitiva stazionaria con tutte le transizioni.
La consistenza strutturale si distingue dalla ripetitività strutturale
- nella ripetitività strutturale è sufficiente che esista una qualsiasi sequenza ripetitiva. Il numero delle marcature può anche cambiare dopo ogni ripetizione.
- nella consistenza strutturale la sequenza ripetitiva deve essere una sequenza stazionaria, ossia il numero complessivo delle marcature è costante. Al termine della sequenza il sistema torna alla marcatura iniziale.
Come capire se una rete è strutturalmente consistente
Posso verificare la consistenza della rete analizzando i T-vettori.
Una rete N è strutturalmente consistente se e solo se esiste un T-vettore y invariante e positivo il cui supporto contenga tutte le transizioni della rete. $$ ||y|| = T = \{ t_1, t_2 , .... , t_n \} $$
Il vettore y è
- positivo se tutti gli elementi sono maggiori di zero.
- T-invariante se il prodotto tra la matrice di incidenza C e il vettore y è un vettore nullo. $$ C \cdot y = 0 $$
Un esempio pratico
Questa rete con tre posti e quattro transizioni è strutturalmente ripetitiva
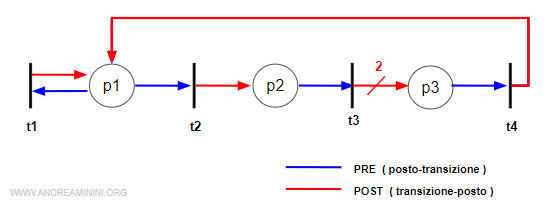
La matrice di incidenza C della rete è
$$ C = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} $$
E' una rete strutturalmente ripetitiva perché esiste almeno un T-vettore crescente y=[1 1 1 1] con elementi positivi.
$$ C \cdot [1 \: 1 \: 1 \: 1 ] = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} \cdot [0 \: 0 \: 0 \: 1 ] \ge 0$$
Per verificare se è anche strutturalmente consistente, devo cercare un vettore T-invariante positivo ossia C·y=0
Trasformo il calcolo vettoriale in un sistema di equazioni.
$$ \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} \cdot [x_1 \: x_2 \: x_3 \: x_4 ] = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} $$
$$ \begin{cases} -x_2 + x_4 = 0 \\ x_2 - x_3 = 0 \\ 2x_3 -x_4 = 0 \end{cases} $$
Cerco di risolvere il sistema con il metodo della sostituzione
$$ \begin{cases} x_4 = x_2 \\ x_2 - x_3 = 0 \\ 2x_3 -x_4 = 0 \end{cases} $$
Sostituisco x4 con x2
$$ \begin{cases} x_2 - x_3 = 0 \\ 2x_3 -x_2 = 0 \end{cases} $$
$$ \begin{cases} x_2 = x_3 \\ 2x_3 = x_2 \end{cases} $$
Il sistema non ha soluzioni. Pertanto, non esiste alcun vettore T-invariante.
Quindi la rete è strutturalmente non consistente.
Nota. Al termine di ogni sequenza ripetitiva la rete ha una marcatura in più rispetto alla precedente. Pertanto, la sequenza ripetitiva non è stazionaria.
La consistenza parziale
Quando il supporto contiene soltanto un sottoinsieme di transizioni si parla di consistenza parziale. $$ ||y|| = T' ⊆ T $$
Nel caso della consistenza strutturale non occorre che il T-vettore sia positivo, può anche ammettere elementi non positivi.
E così via.
