La ripetitivitÓ strutturale della rete
Una rete N è strutturalmente ripetitiva se esiste una marcatura iniziale M0 che genera una sequenza ripetitiva con tutte le transizioni.
La ripetitività strutturale riprende il concetto di ripetitività comportamentale applicandolo anche ad altre marcature della rete.
La differenza tra ripetitività strutturale e comportamentale. La ripetitività comportale viene verificata soltanto nella marcatura iniziale della rete <N,M0>.
Come determinare se una rete è strutturalmente ripetitiva
Per verificare la ripetitività strutturale della rete posso usare i T-vettori.
Una rete N è ripetitiva se e solo se esiste un T-vettore y crescente e positivo il cui supporto contenga tutte le transizioni della rete. $$ ||y|| = T = \{ t_1, t_2 , .... , t_n \} $$
Il vettore y è
- positivo se tutti gli elementi sono maggiori di zero.
- T-crescente se il prodotto tra la matrice di incidenza C e il vettore y è un vettore nullo o positivo. $$ C \cdot y \ge 0 $$
Nota. Nell'insieme dei vettori T-crescenti sono inclusi anche i vettori T-invarianti. E' importante non dimenticarlo.
Un esempio pratico
Prendo in considerazione questa rete con tre posti e quattro transizioni
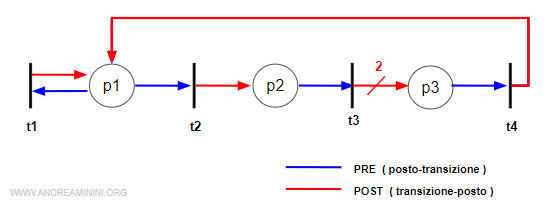
La matrice di incidenza C della rete è
$$ C = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} $$
Esiste un vettore y = [ 1 1 1 1 ] positivo tale che
$$ C \cdot y = \begin{pmatrix} 0 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \\ 1 \end{pmatrix} = [0 \: 0 \: 0 \: 1 ] \ge 0 $$
Pertanto, il vettore y=[1 1 1 1] è T-crescente
Il supporto del vettore y comprende tutte le transizioni della rete
$$ || y || = \{ t_1 \: t_2 \: t_3 \: t_4 \} $$
Posso concludere che la rete marcata è strutturalmente ripetitiva.
Nota. In effetti la rete è molto semplice. Si può facilmente vedere che esiste una sequenza t1t2t3t4 che comprende tutte le transizioni in almeno una marcatura iniziale. In questo caso in tutte le marcature iniziali possibili ma per la ripetitività strutturale ne basterebbe soltanto una.
La ripetitività parziale
Se il supporto contiene soltanto un sottoinsieme di transizioni si parla di ripetitività parziale. $$ ||y|| = T' ⊆ T $$
Nel caso della ripetitività strutturale non è necessario che il T-vettore sia positivo, può avere anche elementi non positivi.
E così via.
