La conservativitÓ strutturale
- Una rete marcata P/T è detta
- strutturalmente conservativa se la rete <N,M0> è conservativa per ogni marcatura iniziale M0.
- strutturalmente strettamente conservatività se la rete <N,M0> è strettamente conservativa per ogni marcatura iniziale M0.
In una rete è strutturalmente conservativa il numero delle marcature non si riduce mai, può però aumentare.
In una rete strutturalmente strettamente conservativa, invece, il numero delle marcature è costante. Non si riduce, né aumenta.
Nota. Il concetto di conservatività strutturale riprende il concetto di conservatività comportamentale e lo estende a tutte le possibili marcature iniziali della rete. Pertanto, la conservatività strutturale implica la conservatività comportamentale ma non è detto l'inverso.
Come capire se una rete è strutturalmente conservativa
Per verificare se una rete è strutturalmente conservativa analizzo i vettori P-invarianti della rete.
- La rete N è strutturalmente strettamente conservativa se il vettore x composto da tutti gli elementi uguali a 1 è invariante.
Esempio. Questa rete è strutturalmente strettamente conservativa
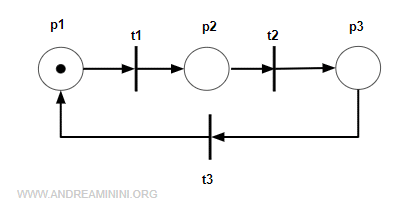
perché il vettore x=[1 1 1] è un vettore P-invariante.
$$ [ 1 \: 1 \: 1 ] \cdot \begin{pmatrix} -1 & 0 & 1 \\ 1 & -1 & 0 \\ 0 & 1 & -1 \end{pmatrix} = [0 \: 0 \:0 ] $$ ossia il vettore x=[1 1 1] moltiplicato per la matrice di incidenza C della rete è un vettore nullo (P-invariante). Il supporto del vettore P-invariante comprende tutti i posti della rete $$ ||x|| = \{ p_1 , p_2, p_3 \} $$ - La rete N è strutturalmente conservativa se esiste un vettore x di interi positivi P-invariante il cui supporto ||x|| contiene tutti i posti della rete. In questo caso il vettore x può assumere anche valori maggiori di 1.
La conservatività strutturale parziale
Se il vettore x è P-invariante ma contiene soltanto alcuni posti, si parla si conservatività strutturale parziale.
Esempio
Prendo in considerazione questa reta marcata
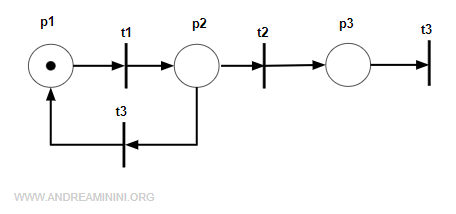
La matrice di incidenza della rete è
$$ C = \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{pmatrix} $$
La rete non è strutturalmente strettamente conservativa perché il vettore x=[1 1 1] non è P-invariante.
$$ [1 \: 1 \: 1 ] \cdot \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{pmatrix} = [ 0 \: 0 \: 0 \: -1 ] \ne [ 0 \: 0 \: 0 \: 0 ] $$
La rete non è nemmeno strutturalmente conservativa perché non esiste alcun vettore x P-invariante con elementi positivi
$$ x \cdot \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{pmatrix} = [ 0 \: 0 \: 0 \: 0 ] $$
Tuttavia, esiste un vettore P-invariante x=[ 1 1 0 ] con alcuni elementi positivi
$$ [1 \: 1 \: 0 ] \cdot \begin{pmatrix} -1 & 0 & 1 & 0 \\ 1 & -1 & -1 & 0 \\ 0 & 1 & 0 & -1 \end{pmatrix} = [ 0 \: 0 \: 0 \: 0 ] $$
Il cui supporto comprende i posti p1 e p2 ma non il posto p3.
$$ ||x|| = \{ p_1 , p_2 \} $$
Pertanto, la rete marcata è strutturalmente conservativa in modo parziale.
Nota. Nel caso della conservatività strutturale parziale non occorre che il vettore x sia positivo. E' sufficiente che sia P-invariante.
La conservatività e limitatezza strutturale
La conservatività strutturale implica la limitatezza strutturale della rete.
Non vale però l'inverso.
Una rete strutturalmente limitata potrebbe non essere strutturalmente conservativa.
Nota. La relazione tra la conservatività e la limitatezza dal punto di vista strutturale è simile alla relazione delle due proprietà dal punto di vista comportamentale.
E così via.
