La limitatezza strutturale della rete
La limitatezza strutturale implica la limitatezza comportamentale della rete marcata <N,M0>, perché la estende per ogni marcatura iniziale M0. Non vale però il contrario.
Nello studio della limitatezza strutturale sono importanti due concetti, quello del posto e della rete strutturalmente limitato.
Posto strutturalmente limitato
Un posto p della rete marcata <N,M0> è strutturalmente limitato se è limitato per ogni marcatura iniziale M0.
Il posto è k-limitato se non può assumere un numero di marche superiori a k marche.
Come capire se il posto è strutturalmente limitata
Il posto è strutturalmente limitato se esiste un vettore P-decrescente x con l'elemento xp>0 dove p è l'indice del posto.
$$ p \in ||x|| $$
Il simbolo ||x|| è l'insieme dei supporti del P-vettore ossia i posti con elementi positivi nel vettore.
Nota. Nell'insieme dei vettori P-decrescenti (x·C≤0) sono inclusi anche i vettori P-invarianti (x·C=0).
Un esempio pratico
Prendo in considerazione una rete con tre posti e tre transizioni.
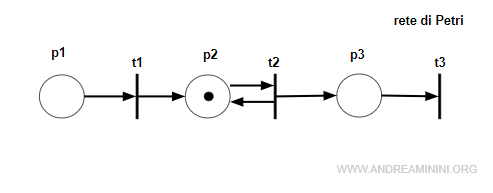
La matrice di incidenza della rete è la seguente:
$$ C = \begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 1 & 0 \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
$$ C = \begin{pmatrix} -1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & -1 \end{pmatrix} $$
Analizzo le prime combinazioni di vettori x·C
$$ [ 1 \: 0 \: 0 ] \cdot C = [-1 \: 0 \: 0 ] \:\:\: P-decrescente $$
$$ [ 0 \: 1 \: 0 ] \cdot C = [1 \: 0 \: 0 ] \:\:\: P-crescente $$
$$ [ 0 \: 0 \: 1 ] \cdot C = [0 \: 1 \: -1 ] \:\:\: $$
$$ [ 1 \: 0 \: 1 ] \cdot C = [-1 \: 1 \: -1 ] \:\:\: $$
$$ [ 1 \: 1 \: 0 ] \cdot C = [0 \: 0 \: 0 ]\:\:\: P-invariante $$
$$ [ 0 \: 1 \: 1 ] \cdot C = [1 \: 1 \: -1 ] \:\:\: $$
$$ [ 1 \: 1 \: 1 ] \cdot C = [0 \: 1 \: -1 ] \:\:\: P-crescente $$
Quindi, sono P-decrescenti i vettori x=[1 0 0] e x=[1 1 0]
Nel caso del vettore x=[1 0 0] l'unico supporto e p1
$$ ||x|| = \{ p_1 \} $$
Nel caso del vettore x=[1 1 0] i supporti sono p1 e p2.
$$ ||x|| = \{ p_1 \: p_2 \} $$
Pertanto, i posti p1 e p2 sono strutturalmente limitati.
Il posto p3 invece non è strutturalmente limitato.
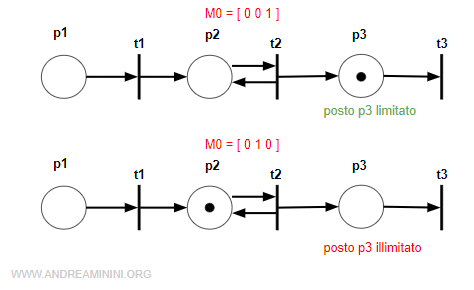
Differenza tra limitatezza comportamentale e strutturale. Questo esempio dimostra anche la mancanza di causalità della limitatezza comportale nei confronti della limitatezza strutturale. Secondo l'analisi comportamentale con la marcatura iniziale M0=[0 0 1] il posto p3 è limitato perché la transizione può scattare una sola volta riducendo il numero delle marche in p3. Tuttavia, secondo l'analisi strutturale il posto p3 non è anche strutturalmente limitato. Questo vuol dire che il posto p3 potrebbe essere limitato per alcune marcature iniziali (es. M0=[0 0 1]) ma non in altre marcature iniziali (es. M0=[0 1 0]).
Rete strutturalmente limitata
Una rete N è strutturalmente limitata se ogni posto della rete <N,M0> è strutturalmente limitato.
Come verificare se la rete è strutturalmente limitata
La rete è strutturalmente limitata se esiste almeno un vettore p-decrescente x con gli elementi xi>0.
$$ P = ||x|| $$
dove P=[p1,....,pi] è il vettore dei posti della rete.
Il simbolo ||x|| è l'insieme dei supporti del P-vettore ossia i posti con elementi positivi nel vettore.
Nota. Nell'insieme dei vettori P-decrescenti (x·C≤0) sono inclusi anche i vettori P-invarianti (x·C=0).
Esempio1
La rete dell'esempio precedente ha tre posti

Il vettore P dei posti della rete è il seguente:
$$ P = \{ p_1 \: p_2 \: p_3 \} $$
I posti p1 e p2 della rete sono posti strutturalmente limitati.
Il posto p3 invece non è strutturalmente limitato.
La rete ha due vettori P-decrescenti [1 0 0] e [1 1 0] con i seguenti supporti
$$ || \:x=[1 \: 0 \:0] \: || = \{ p_1 \} \ne P $$
$$ || \:x=[1 \: 1 \:0] \: || = \{ p_1 \: p_2 \} \ne P $$
Nessuno dei due supporti è uguale al vettore dei posti P.
Pertanto, la rete non è strutturalmente limitata.
Esempio 2
Prendo in considerazione quest'altra rete leggermente diversa dalla precedente.
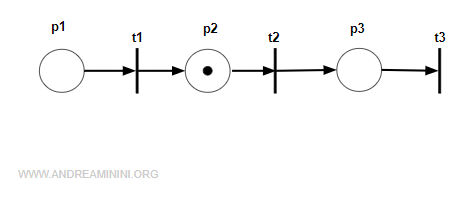
La matrice di incidenza della rete è la seguente:
$$ C = \begin{pmatrix} -1 & 0 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & 1 \end{pmatrix} $$
Il vettore x con tutti i posti della rete è [1 1 1].
Lo moltiplico per la matrice di incidenza per verificare se è un vettore P-decrescente.
$$ [1 \: 1 \: 1] \cdot \begin{pmatrix} -1 & 0 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & 1 \end{pmatrix} = [ 0 \: -1 \: 0 ] ≤ 0 $$
Il vettore x=[1 1 1] è effettivamente un vettore P-decrescente.
Pertanto, la rete è strutturalmente limitata.
Nota. Questo equivale a dire che tutti i posti della rete sono strutturalmente limitati.
E così via.
