Stato bloccante in un automa
In un automa a stati finiti uno stato x2 è detto bloccante se è raggiungibile dallo stato x1 ma non è co-raggiungibile.
Uno stato è raggiungibile se esiste una produzione in grado di far transitare l'automa dallo stato x1 allo stato x2.
E' co-raggiungibile se esiste anche una produzione inversa in grado di far transitare l'automa dallo stato x2 allo stato x1.
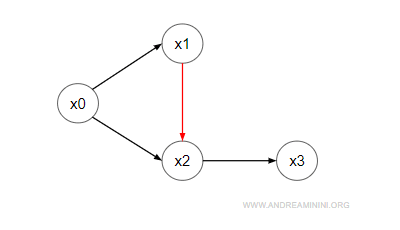
In un digrafo lo stato bloccante è individuato da un cammino orientato da x1 a x2 e dalla mancanza di un cammino inverso da x2 a x1.
Nel caso in cui lo stato bloccante non abbia altri archi in uscita è anche uno stato morto.
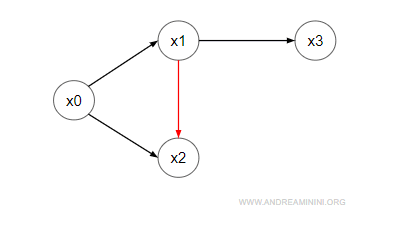
Nota. Lo stato bloccante e lo stato morto sono due proprietà diverse. Uno stato è morto se non ha transizioni in uscita per qualsiasi evento. Nello stato bloccante, invece, manca il cammino verso un altro nodo da cui è raggiungibile. Uno stato bloccante non è detto che sia morto. Inoltre, uno stato morto non è bloccante se è uno stato finale.
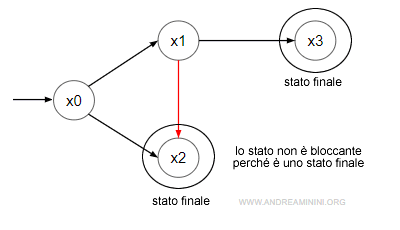
Automa AFD non bloccante
Un automa deterministico a stati finiti G (AFD) è non bloccante se il linguaggio generato L è uguale al linguaggio accettato Lm e quest'ultimo è chiuso per prefisso. $$ L(G) = \bar{L}_m(G) $$
Dimostrazione
Il linguaggio generato L è l'insieme delle parole generate dall'automa.
Il linguaggio accettato Lm è l'insieme di parole w che collegano lo stato iniziale con uno stato finale dell'automa.
Un linguaggio è chiuso per prefisso se anche i prefissi delle sue parole appartengono al linguaggio stesso.
Nota. Il linguaggio generato L è sempre chiuso per prefisso. Non è però detto che il linguaggio accettato Lm sia chiuso per prefisso.
Se il linguaggio generato eguaglia il linguaggio accettato Lm, vuol dire che ogni produzione conduce a uno stato finale a partire dallo stato iniziale.
$$ L=L_m $$
Se il linguaggio accettato è chiuso per prefisso
$$ L_m=\bar{L}_m $$
ogni parola generata u di L(G) è un prefisso di una parola accettata v di Lm.
$$ uv \in L_m(G) $$
Per ogni stato raggiungibile d(x0,u) esiste una transizione d*(x,v) dove x è uno stato finale.
Ogni stato raggiungibile x è anche co-raggiungibile.
Quindi, in nessun caso una parola del linguaggio generato L può condurre a uno stato diverso dallo stato finale dell'automa.
In tali circostanze non può verificarsi nessun blocco.
Nota. Questa regola vale soltanto per gli automi a stati finiti deterministici AFD. Non vale per gli automi non deterministici AFN perché una stessa parola w può essere associata a produzioni diverse.
Esempio
Questo è un algoritmo bloccante.
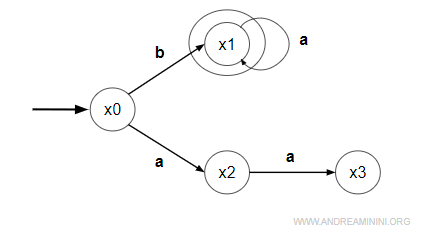
Il linguaggio accettato dall'automa è composto dalle seguenti parole
$$ L_m(G) = \{ ba^n \} $$
Il linguaggio generato è
$$ L(G) = \{ ε, a, aa \} U \{ ba^n \} $$
Il linguaggio accettato chiuso per prefisso è
$$ \bar{L}_m(G) = \{ ε \} U \{ ba^n \} $$
Il linguaggio accettato chiuso per prefisso è soltanto un sottoinsieme del linguaggio generato.
$$ \bar{L}_m(G) ⊂ L(G) $$
Quindi l'automa è bloccante.
E così via.
