Automi a stati finiti non deterministici
Un automa a stati finiti non deterministico AFN è una 5-upla $$ G=(X,E,Δ,x_0,X_n) $$
Le componenti dell'automa sono
- X è un insieme finito di stati
- E è un insieme finito di eventi
- Δ è la relazione di transizione da uno stato x a un altro in conseguenza di un evento e
dove $$ Δ ⊆ X x E* x X$$
- x0 è lo stato iniziale
- Xn è l'insieme degli stati finali (stati marcati)
La differenza tra automi deterministici e non deterministici
La struttura degli automi a stati finiti deterministici (AFD) e non deterministici (AFN) è simile. Anche la rappresentazione grafica è analoga.
Tuttavia, ci sono importanti differenze.
- Automa deterministico
In un automa deterministico AFD o DFA (Deterministic Finite Automaton) ogni relazione di transizione ha uno stato di destinazione per ogni simbolo (evento). Non possono esserci relazioni di transizione nello stesso stato che usano lo stesso simbolo. - Automa non deterministico
In un automa non deterministico NFA (Non Deterministic Finite Automaton) una relazione di transizione può avere uno o più stati di destinazione con lo stesso simbolo (evento).Nota. Quando l'automa incontra due transizioni associate allo stesso evento a partire da uno stato, li segue entrambi come eventi parzialmente osservabili. In pratica, non sa ancora quale sia vero e quale sia falso. Quindi, li analizza entrambi.
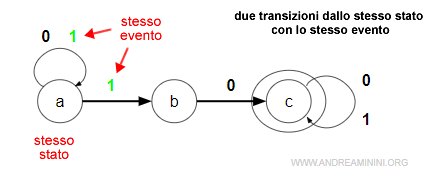
Inoltre, la relazione Δ di transizione non è una funzione perché in un automa non deterministico (AFN) una stessa parola w può condurre a stati di destinazione x diversi.
Un esempio pratico
Ho un automa non deterministico che lavora con un alfabeto binario {0,1}.
L'automa analizza una stringa composta da 0 e 1.
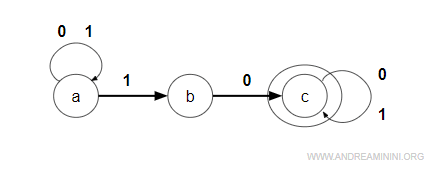
La funzione di transizione è
$$ Δ = \{ (a,0,a) , (a,1,a) , (a,1,b) , (b,0,c), (c,0,c) , , (c,1,c) \} $$
Questo automa riconosce le stringhe con una sequenza interna composta almeno una volta dalla sottostringa "01".
Provo ad analizzare la stringa "11"
Primo evento
Il primo evento è il simbolo 1 ossia il primo carattere della stringa 11.
L'automa non deterministico resta nello stato A e contemporaneamente passa nello stato B.
E' come se lanciasse due processi in esecuzione in background.
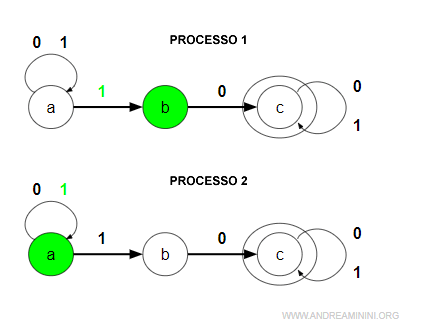
Nota. Nell'automa AFN da uno stato possono uscire più transizioni, diverse tra loro, che usano lo stesso simbolo (evento). L'automa attiva più stati e li elabora separatamente.

Secondo evento
L'evento successivo è il simbolo 1. E' il secondo carattere della stringa "11".
Il nuovo evento è analizzato sia nel nodo A che nel nodo B.
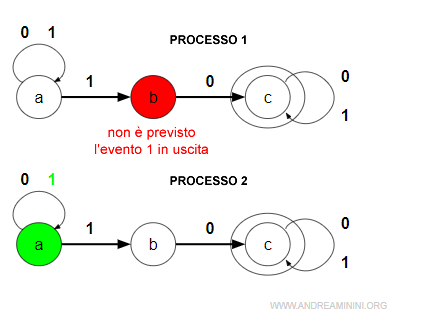
- Il processo nel nodo A continua a girare perché è previsto l'evento (1). In questo caso permane nello stesso nodo A,
- Il processo nel nodo B viene eliminato perché non è previsto l'evento (1) in uscita.
Nota. Nello stato B non c'è nessuna transizione con l'evento 1. Manca anche il collegamento "cappio" con se stesso. Il verificarsi dell'evento 1 fa cadere l'ipotesi stessa sulla quale è nato il cammino. Per questa ragione viene interrotto.
Le epsilon transizioni ε
Un automa a stati finiti non deterministico prevede anche le transizioni ε.
Cosa sono le transizioni ε
Una transizione ε è una transizione etichettata con la parola vuota ε. Sono eventi silenziosi che fanno passare l'automa direttamente da uno stato all'altro senza che si verifichi nessun evento.
Esempio
A partire da x0 la parola ab conduce sia a x1 che a x2.
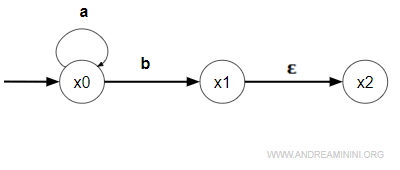
Le produzioni dell'automa
Una produzione è una sequenza di eventi che conduce l'automa da uno stato a un altro stato.
Una produzione equivale a una parola w
$$ w=e_1e_2...e_n $$
dove ogni lettera ei indica il simbolo di un evento che determina la transizione dello stato.
$$ x_n = Δ(x_{n-1},w) $$
Gli eventi in una parola w possono anche essere ripetuti.
Inoltre, la produzione di un automa AFN può contenere anche transizioni ε.
Esempio. In questo esempio il passaggio dallo stato X0 allo stato X3 è realizzato dalla produzione 01.

La chiusura transitiva e riflessiva
In un automa AFN la chiusura transitiva e riflessiva della relazione Δ è una relazione Δ* tale che (x,w,x')∈Δ* se esiste una produzione che a partire da x raggiunge x' con una parola w.
Perché sono detti automi non deterministici
Sono detti automi non deterministici perché la presenza dell'e-transizione rende una parola di eventi w, generata a partire da uno stato x, associabile a diverse produzioni.
Pertanto, una stessa parola w da uno stato x0 potrebbe avere un'evoluzione diversa e condurre a stati di destinazione differenti.
La parola w di eventi è l'input del sistema mentre la produzione è l'evoluzione (comportamento) del sistema in output.
Un esempio pratico
Questo percorso va da x0 a x3 con la parola w=aba
I passaggi di stato sono tre (x0,a,x0), (x0,b,x2), (x2,a,x3)
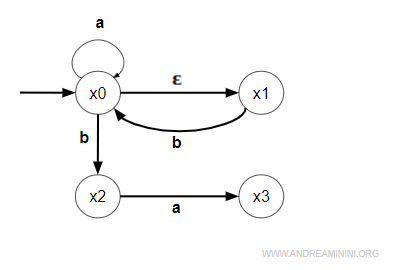
Tuttavia, la stessa parola w=aba potrebbe portare dallo stato x0 allo stato x0 con una diversa produzione.
In questo caso i passaggi di stato sono quattro: (x0,a,x0), (x0,ε,x2), (x2,b,x0) , (x0,a,x0)
Nota. In un sistema AFN la lunghezza della parola w potrebbe anche essere inferiore al numero di transizioni della produzione, perché la parola vuota ε genera una transizione fisica di stato senza far parte della parola w.
Il linguaggio
Il linguaggio di un automa AFN è composto da parole.
Esistono due tipologie di parole
- Parola generata
Una parola w è generata dall'automa se esiste una produzione che genera la parola w a partire dallo stato iniziale x0 in grado di raggiungere lo stato x (x0,w,x). - Parola accettata
Una parola w è accettata dall'automa se esiste una produzione che genera la parola w partire dallo stato iniziale x0 in grado di raggiungere uno stato finale xf (x0,w,xf).
Nota. Nel caso degli automi non deterministici una stessa parola w può condurre a stati di destinazione diversi. Quindi, alcune potrebbero essere generate e altre accettate. Per essere definita "accettata" è sufficiente che ci sia almeno una produzione in grado di raggiungere uno stato finale a partire dallo stato iniziale.
Un insieme di parole w compongono un linguaggio.
Pertanto, esistono due tipologie di linguaggi
- Il linguaggio generato
E' il linguaggio L(G) composto da tutte le parole generate dall'automa. - Il linguaggio accettato (o marcato)
E' il linguaggio Lm(G) composto da tutte le parole accettate dall'automa.
Il linguaggio accettato è un sottoinsieme del linguaggio generato. $$ Lm(G) ⊆ L(G) $$
Tutti i linguaggi accettati dall'automa formano la classe £AFN.
Osservazioni
Alcune osservazioni e note a margine sugli automi non deterministici
- Ogni automa non deterministico può essere trasformato in un automa deterministico
Un automa non deterministico (NFA) può essere trasformato in un automa deterministico (DFA) attraverso l'algoritmo di determinizzazione. Questo algoritmo crea uno stato del DFA per ogni insieme di stati dell'NFA e per tutte le possibili transizioni. Il risultato è un automa DFA, molto più grande dell'automa NF, che accetta lo stesso linguaggio dell'NFA originale, ma ha una struttura che permette una sola transizione per ogni stato e simbolo dell'alfabeto. Come conseguenza deduco che gli automi NFA e DFA accettano lo stesso linguaggio regolare.
E così via.
