Come funziona un automa
Come funziona un automa
Prendo in considerazione un automa a stati finiti deterministico (AFD).
$$ S = (X,E,δ,x_0,X) $$
Un automa S è un generatore di sequenze di eventi, create utilizzando un alfabeto E.
L'alfabeto E è l'insieme degli eventi del sistema.
Nota. L'insieme degli eventi (alfabeto) è paragonabile all'insieme delle parole che si possono formare con le lettere dell'alfabeto. Ogni lettera indica un evento.
Una sequenza di eventi forma una parola (w)
L'insieme delle parole compone un linguaggio L(S) detto linguaggio generato dal sistema.
Tuttavia, soltanto alcune parole modificano effettivamente il comportamento del sistema, ossia sono associate a operazioni dell'automa.
Questo sottoinsieme di parole forma il linguaggio accettato dal sistema Lm(S).
L'automa può assumere un insieme di stati X durante il funzionamento.
Lo stato x0 è lo stato iniziale del sistema.
Il passaggio da uno stato all'altro è regolato dalla funzione di transizione degli stati δ.
Nota. Esistono diverse tipologie di sistemi SED. In questo caso ho considerato un automa a stati finiti. Il controllo supervisivo può comunque essere applicato a qualsiasi altra tipologia di sistema a eventi discreti.
Un esempio pratico
Questo automa S ha un insieme degli stati X={x0,x1,x2,x3}.
Lo stato x0 è lo stato iniziale (macchina spenta). Gli altri stati sono x1 (macchina accesa), x2 (macchina al lavoro), x3 (macchina in manutenzione).
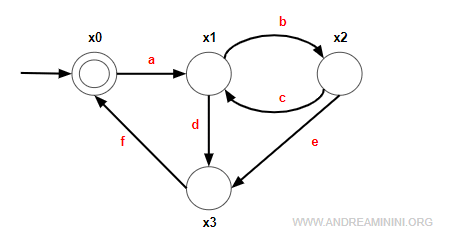
Il sistema è caratterizzato da tre eventi {a,b,c,d,e,f}.
- a = accendi la macchina
- b = inizia la lavorazione
- c = ferma la lavorazione
- d = metti in stand-by
- e = guasto o errore
- f = esegui la manutenzione e resetta la macchina
Quindi, l'insieme degli eventi ( alfabeto ) è l'insieme degli eventi
$$ E = \{ a,b,c,d, e, f \} $$
Gli eventi formano delle parole associate a specifiche operazioni dell'automa.
Il linguaggio generato è composto da sequenze di eventi possibili nel sistema.
$$ L = \{ a,ab,abc, abcd, ... \} $$
Il linguaggio accettato è composto soltanto dalle sequenze associate a un'operazione del sistema
$$ L_m = \{ a,ab, abc, ad, ... \} $$
Nota. Ad esempio, la sequenza a indica l'accensione della macchina, la sequenza ab la messa in moto della macchina, la sequenza abc la messa in pausa, la sequenza abcdf lo spegnimento dopo la lavorazione, la sequenza adf la manutenzione, la sequenza abced il guasto e la riparazione della macchina, ecc.
Il passaggio da uno stato all'altro è definito dalla funzione di transizione
$$ x_d=δ(x,s) $$
Dove x è lo stato di origine, xd è lo stato di destinazione ed s∈E è l'evento che genera la transizione.
$$ x_1=δ(x_0,a) \\ x_2=δ(x_1,b) \\ x_1=δ(x_2,c) \\ x_3=δ(x_1,d) \\ x_3=δ(x_2,e) \\ x_0=δ(x_3,f) $$
Le parole (sequenze di eventi) sono composte a partire dallo stato iniziale.
$$ x_1=δ(x_0,a) \\ x_2=δ(x_0,ab) \\ x_3=δ(x_0,ad) \\ x_3=δ(x_0,abcd) \\ x_3=δ(x_0,abe) \\ \vdots $$
L'insieme degli eventi attivi A indica gli stati attivi dopo una parola w (sequenza di eventi) o da un particolare stato x del sistema.
$$ A(w) = \{s \in E \: | \: w \in L \} $$
$$ A(x) = \{s \in E \: | \: δ(x,s)! \} $$
Nota. Il simbolo ! dopo δ(x,s) indica che la transizione è definita nella coppia (x,s) ossia è ammessa.
Ad esempio, gli eventi attivi dopo la sequenza di eventi w = ab sono gli eventi {c,e}.
Dove c=ferma la lavorazione ed e=guasto della macchina
$$ A(ab) = \{ c, e \} $$
Allo stesso modo gli eventi attivi nello stato x2 sono gli eventi {c,e}.
$$ A(x_2) = \{ c, e \} $$
E' un modo diverso per ottenere la stessa informazione a partire da un dato iniziale differente (sequenza di eventi o stato del sistema).
Nota. L'insieme degli stati attivi dopo una sequenza w o da uno stato x coincide se x è raggiungibile da x0 tramite la parola w. $$ A(ab) = A(x_2) = \{ c, d \} $$ perché in questo caso x2 è raggiungibile da x0 tramite la sequenza di eventi w=ab. $$ x_2=δ(x_0,ab) $$
E così via.
