Come trasformare un automa NFA in DFA

Qualsiasi automa a stati finiti non deterministico (NFA) può essere trasformato in un automa deterministico (DFA).

L'automa risultate esplora tutte le possibili transizioni di stato ed è molto più grande del corrispondente automa NFA.

Questo significa che gli automi a stati finiti deterministici o non deterministici sono equivalenti perché accettano lo stesso linguaggo regolare.

Un esempio pratico

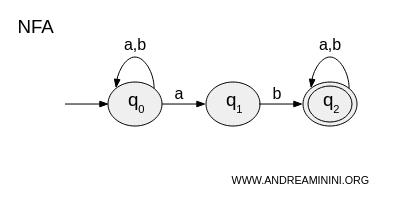
Considero questo semplice automa a stati finiti non deterministico (NFA) con tre stati \(\{q_0, q_1, q_2\}\) e un alfabeto a due simboli \(\{a, b\}\) dove \( q_0 \) è lo stato iniziale e \( q_2 \) è lo stato di accettazione.

Per prima cosa identifico i sottoinsiemi degli stati dell'NFA calcolando l'insieme delle parti.

I sottoinsiemi sono:

\[
\emptyset, \{q_0\}, \{q_1\}, \{q_2\}, \{q_0, q_1\}, \{q_0, q_2\}, \{q_1, q_2\}, \{q_0, q_1, q_2\}
\]

Li dispongo senza un ordine preciso per poterli collegare successivamente

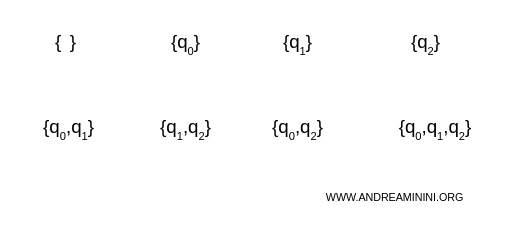
Lo stato iniziale del DFA

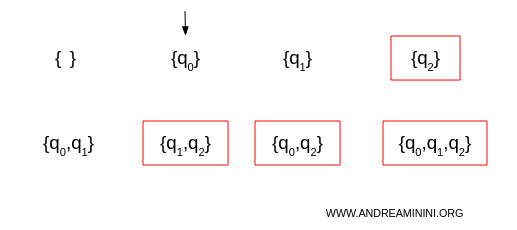
Individuo l'insieme degli stati raggiungibili dallo stato iniziale senza leggere alcun simbolo.

In questo caso lo stato iniziale del DFA è solo lo stato \(\{q_0\}\) perché non sono transizioni vuote.

Gli stati accettanti del DFA

I sottoinsiemi che contengono lo stato di accettazione del NFA \(q_2\) sono gli stati accettanti del DFA:

$$ \{q_2\}, \{q_0, q_2\}, \{q_1, q_2\}, \{q_0, q_1, q_2\} $$ 

Li indico in rosso

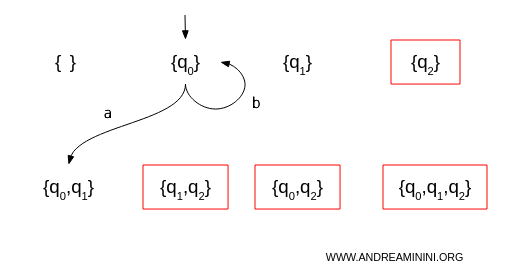
La funzione di transizione del DFA

A questo punto costruisco la funzione di transizione del DFA considerando tutti i sottoinsiemi:

• Da \(\{q_0\}\):
  Con \(a\): \(\delta(\{q_0\}, a) =  \{q_0, q_1\}\)
  Con \(b\): \(\delta(\{q_0\}, b) =  \{q_0\}\)
  
• Da \(\{q_0, q_1\}\):
  Con \(a\): \(\delta(\{q_0, q_1\}, a) = \delta(q_0, a) \cup \delta(q_1, a) = \{q_0, q_1\}\)
  Con \(b\): \(\delta(\{q_0, q_1\}, b) = \delta(q_0, b) \cup \delta(q_1, b) = \{q_0, q_2\}\)
  
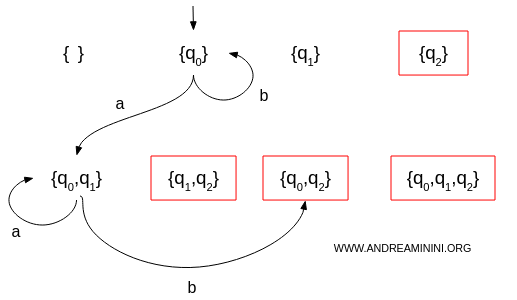
• Da \(\{q_0, q_2\}\):
  Con \(a\): \(\delta(\{q_0, q_2\}, a) = \delta(q_0, a) \cup \delta(q_2, a) = \{q_0, q_1, q_2\}\)
  Con \(b\): \(\delta(\{q_0, q_2\}, b) = \delta(q_0, b) \cup \delta(q_2, b) = \{q_0, q_2\}\)
  
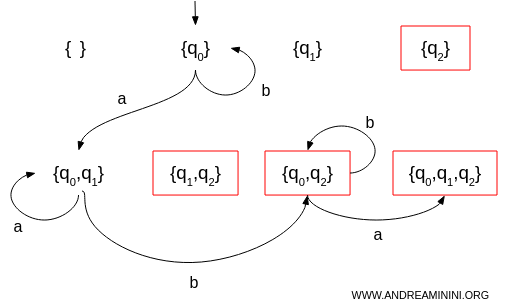
• Da \(\{q_0, q_1,q_2\}\):
  Con \(a\): \(\delta(\{q_0, q_1, q_2\}, a) =\delta(q_0, a) \cup \delta(q_1, a) \cup \delta(q_2, a) = \{q_0, q_1, q_2\}\)
  Con \(b\): \(\delta(\{q_0, q_1, q_2\}, b) =\delta(q_0, b) \cup \delta(q_1, b) \cup \delta(q_2, b) = \{q_0, q_2\}\)
  

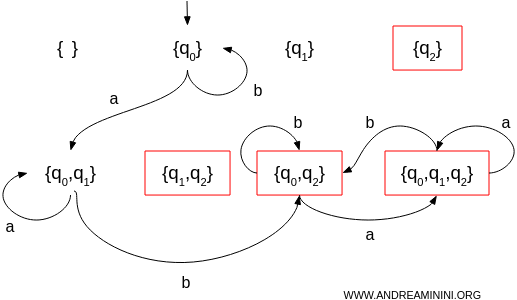
Gli altri sottoinsiemi (\( \{ \ \}\), \{q_1\}\), , \{q_2\}\), \(\{q_1, q_2\}\) non vengono raggiunti in questo esempio con i simboli di input dati, quindi non influenzano il DFA finale.

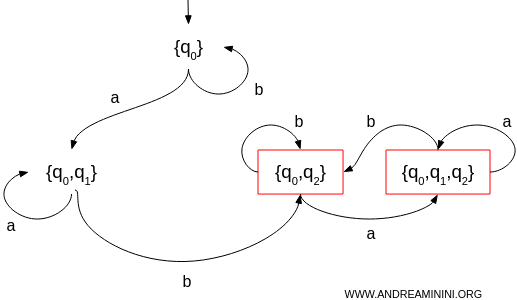
DFA risultante

Il DFA risultante ha i seguenti stati:

$$ Q =  \{ \emptyset, \{q_0\}, \{q_0, q_1\}, \{q_0, q_2\},  \{q_0, q_1, q_2\} \} $$

Lo stato iniziale è lo stato  \(\{q_0\}\)

Gli stati accettanti sono i seguenti:

$$ F = \{ \  \{q_0, q_2\}, \{q_0, q_1, q_2\} \ \} $$

La funzione di transizione è la seguente:

- \(\delta(\{q_0\}, a) = \{q_0, q_1\}\)
- \(\delta(\{q_0\}, b) = \{q_0\}\)
- \(\delta(\{q_0, q_1\}, a) = \{q_0, q_1\}\)
- \(\delta(\{q_0, q_1\}, b) = \{q_0, q_2\}\)
- \(\delta(\{q_0, q_2\}, a) = \{q_0, q_1, q_2\}\)
- \(\delta(\{q_0, q_2\}, b) = \{q_0, q_2\}\)
- \(\delta(\{q_0, q_1, q_2\}, a) = \{q_0, q_1, q_2\}\)
- \(\delta(\{q_0, q_1, q_2\}, b) = \{q_0, q_2\}\)

Il grafo dell'automa DFA equivalente è:

Dove gli stati in rosso sono gli stati di accettazione del DFA equivalente.

Questo esempio mostra come un NFA con transizioni non deterministiche può essere convertito in un DFA che simula tutte le possibili computazioni dell'NFA.