Stato raggiungibile e co-raggiungibile in un automa
Lo stato raggiungibile
In un automa uno stato x2 è raggiungibile dallo stato x1 se è definita la transizione δ(x1,w)=x2 con una parola w, ossia con una serie di eventi.
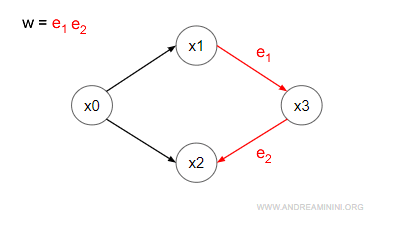
La raggiungibilità dello stato equivale all'esistenza di un cammino orientato dal nodo x1 al nodo x2 in un grafo orientato (digrafo).
Lo stato co-raggiungibile
In un automa uno stato x2 è detto co-raggiungibile verso x1 , se è definita una transizione δ(x2,w')=x1 con una parola w'.
In un digrafo questo vuol dire che esiste un cammino orientato da x2 a x1 (co-raggiungibilità).
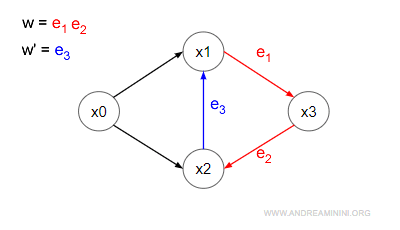
Il cammino w' congiunge x2 con x1.
Quindi x2 è co-raggiungibile verso x1.
Lo stato bloccante. Lo stato x2 è detto bloccante se è raggiungibile dallo stato iniziale ma non co-raggiungibile da uno stato finale.
La non raggiungibilità dello stato
Lo stato x2 è detto non raggiungibile da x1 se non esiste una parola w (sequenza di eventi) in grado di portare l'automa dallo stato x1 allo stato x2.
In questo caso la transizione x2=δ(x1,w) non è definita.
$$ x_2=δ(x_1,w)! $$
In un digrafo questo equivale all'assenza di un cammino orientato dal nodo x1 al nodo x2.
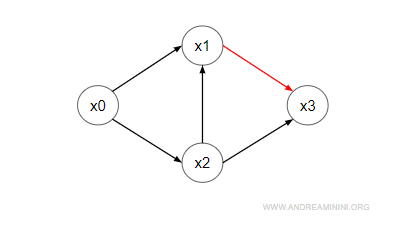
Nel precedente digrafo lo stato x2 è non raggiungibile dallo stato x1 perché la direzione degli archi è opposta.
E così via.
