Sintesi modulare
La sintesi modulare è la costruzione di un sistema complesso composto da più sottosistemi semplici detti moduli.
In un automa DFA i moduli sono collegati tra loro tramite composizione concorrente.
Ogni modulo è un automa semplice, ha un proprio alfabeto e i propri stati.
$$ E' = \{ a,b \} \\ E" = \{ b,c \} $$
L'alfabeto complessivo è dato dall'unione di tutti gli alfabeti dei moduli.
$$ E=E'∪E" = \{ a,b,c \} $$
Nota. Se i moduli sono automi deterministici (DFA) allora anche la sintesi modulare è un automa deterministico. Tuttavia, le proprietà dei moduli non si trasferiscono alla sintesi. Ad esempio, se i moduli sono rifiniti, non è detto che la sintesi sia un automa rifinito, potrebbe anche essere bloccante e viceversa.
Gli eventi sincronizzati e non sincronizzati
L'alfabeto complessivo di un automa non è detto che sia un insieme delle parti perché alcuni alfabeti potrebbero intersecarsi tra loro.
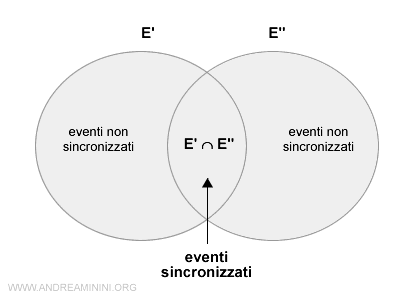
Quindi alcuni simboli dell'alfabeto (eventi) sono presenti in più moduli. $$ E' ⋂ E" $$
Questo mi permette di distinguere tra gli eventi sincronizzati e non.
- Eventi sincronizzati
Sono gli eventi che appartengono a due o più alfabeti (E' ⋂ E"). Questi eventi dipendono anche dallo stato simultaneo che si presenta in due o più moduli. - Eventi non sincronizzati
Sono gli eventi che appartengono a un solo alfabeto. Determinano la transizione da uno stato all'altro in un modulo, indipendentemente dallo stato negli altri moduli.
I sottoinsiemi sincronizzati e non sincronizzati formano una partizione dell'alfabeto complessivo.
La composizione concorrente
La composizione concorrente di due moduli G' e G" è un automa G con un linguaggio generato e un linguaggio accettati uguale alla composizione concorrente dei linguaggi generati dai moduli che lo compongono. $$ L(G) = L(G') || L(G") $$ $$ L_m(G) = L_m(G') || L_m(G") $$
Come creare un automa modulare
Per creare un automa modulare ho bisogno di almeno due automi G' e G".
- Unisco i due alfabeti E' e E" in un unico alfabeto E
- Seleziono come stato iniziale il prodotto cartesiano (x'0,x"0) degli stati iniziali dei due automi.
- Creo un insieme X = {} con gli stati esplorati
- Creo un insieme W = { } con gli stati da esplorare
- Inserisco lo stato (x'0,x"0) in W
- Estraggo uno stato w da esplorare da W
- Controllo le transizioni in uscita dallo stato w per ogni evento dell'alfabeto E={a,b,c}
- Se l'evento è sincronizzato
x'=(x',e)
x"=(x",e) - Se l'evento non è sincronizzato
se e∈E' → x'=(x',e)
se e∈E"→ x"=(x",e)
- Se l'evento è sincronizzato
- Se le transizioni precedenti sono definite, aggiungo la transizione d(x,e)=(x',x") alla sintesi modulare. Poi aggiungo lo stato (x',x") in W nell'insieme degli stati da esplorare se non è già presente in X e in W.
Nota. Se le transizioni non sono definite (a seconda del caso) non aggiungo alcun nuovo stato alla sintesi modulare, né agli stati da esplorare.
- Estraggo un nuovo stato dall'insieme degli da esplorare W e ricomincio la procedura.
- L'algoritmo termina quando l'insieme W è vuoto.
Un esempio pratico
Voglio usare i due automi come moduli di un automa complesso G tramite la procedura di sintesi modulare.
Ho due automi semplici G' e G".
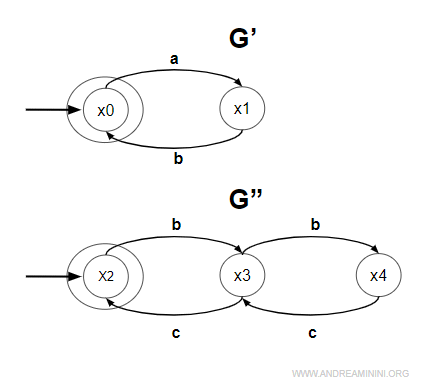
I due automi hanno alfabeti diversi
$$ E' = \{ a,b \} \\ E" = \{ b,c \} $$
L'alfabeto complessivo è
$$ E=E'∪E" = \{ a,b,c \} $$
Quindi l'evento b è un evento sincronizzato mentre gli eventi a,c non lo sono.
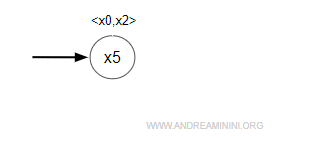
Scelgo come stato iniziale dell'algoritmo complesso il prodotto cartesiano degli stati iniziali x0 e x2 dei due automi semplici.
$$ x_5 = < x_0, x_2> $$
Il digrafo della sintesi modulare comincia così
Creo due insiemi X e W.
In X inserisco i gli stati analizzati mentre in W gli stati da esplorare.
Inizialmente in W inserisco lo stato iniziale x5 = <x0,x2>.
$$ X = \{ \} \\ W = \{x_5\} $$
1] Analisi del primo stato <x0,x2>
Prelevo uno stato da W, lo elimino da W e lo sposto in X.
$$ X = \{ x_5 \} \\ W = \{ \} $$
E' lo stato x5.
$$ x_5 = < x_0, x_2> $$
Poi analizzo le transizioni dallo stato per ogni evento dell'alfabeto.
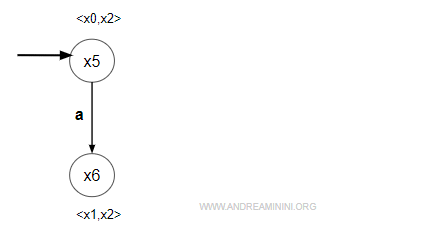
- evento "a" = non simmetrico
L'evento "a" appartiene soltanto all'automa G'. Pertanto, modifico soltanto il primo membro del prodotto cartesiano <x0,x2> $$ δ(x_0, a) = x_1 $$ La transizione è definita. Ho così trovato un nuovo stato <x1,x2> dell'automa di sintesi $$ x_6 = <x_1, x_2> $$ Lo aggiungo agli stati da visitare W = { x6 }.
- evento "b" = simmetrico
L'evento "b" è simmetrico perché appartiene sia a G' che a G". Quindi, devo modificare entrambi i membri del prodotto cartesiano <x0,x2> $$ δ(x_0, b) = ND \\ δ(x_2, b) = ND $$ Le transizioni non sono definite. Non faccio nulla. - evento "c" = non simmetrico
L'evento "c" non è simmetrico e appartiene soltanto all'automa G". Pertanto, modifico solo il secondo membro del prodotto cartesiano <x0,x2> $$ δ(x_2, c) = ND $$ La transizione non è definita in G". Non faccio nulla
2] Analisi dello stato <x1,x2>
Prelevo uno stato da W, lo elimino da W e lo sposto in X.
$$ X = \{ x_5, x_6 \} \\ W = \{ \} $$
E' lo stato x6.
$$ x_6 = < x_1, x_2> $$
Poi analizzo le transizioni dallo stato per ogni evento dell'alfabeto.
- evento "a" = non simmetrico
Modifico soltanto il primo membro del prodotto cartesiano <x1,x2> $$ δ(x_1, a) = ND $$ Non è definito. Non faccio nulla. - evento "b" = simmetrico
Modifico entrambi i membri del prodotto cartesiano <x1,x2> $$ δ(x_1, b) = x_0 \\ δ(x_2, b) = x_3 $$ Le transizioni sono definite e puntano verso il prodotto cartesiano <x0,x3>. Non esiste ancora. Quindi creo un nuovo stato x7=<x0,x3> e lo aggiungo in W.
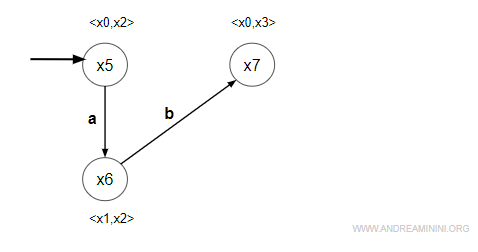
- evento "c" = non simmetrico
Modifico solo il secondo membro del prodotto cartesiano <x1,x2> $$ δ(x_2, c) = ND $$ La transizione non è definita in G". Non faccio nulla
3] Analisi dello stato <x0,x3>
Prelevo uno stato da W, lo elimino da W e lo sposto in X.
$$ X = \{ x_5, x_6, x_7 \} \\ W = \{ \} $$
E' lo stato x7.
$$ x_7 = < x_0, x_3> $$
Poi analizzo le transizioni dallo stato per ogni evento dell'alfabeto.
- evento "a" = non simmetrico
Modifico soltanto il primo membro del prodotto cartesiano <x0,x3> $$ δ(x_0, a) = x_1 $$ E' definita. Sostituisco x1 a x0 e ottengo <x1,x3>. Il prodotto cartesiano non esiste ancora. Quindi creo un nuovo stato x8=<x1,x3> e lo aggiungo a W.
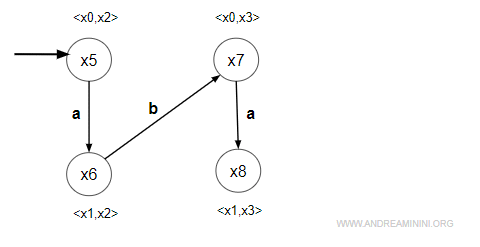
- evento "b" = simmetrico
Modifico entrambi i membri del prodotto cartesiano <x0,x3> $$ δ(x_0, b) = ND \\ δ(x_3, b) = x_4 $$ Una transizione non è definita. Quindi, non faccio nulla. - evento "c" = non simmetrico
Modifico solo il secondo membro del prodotto cartesiano <x0,x3> $$ δ(x_3, c) = x_2 $$ E' definita. Sostituisco x2 a x3 e ottengo <x0,x2>. Il prodotto cartesiano esiste già, è lo stato x5. Quindi aggiungo soltanto una transizione per "c" da x7 a x5.
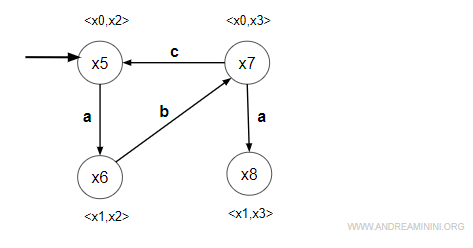
4] Analisi dello stato <x1,x3>
Prelevo uno stato da W, lo elimino da W e lo sposto in X.
$$ X = \{ x_5, x_6, x_7, x_8 \} \\ W = \{ \} $$
E' lo stato x8.
$$ x_8 = < x_1, x_3> $$
Poi analizzo le transizioni dallo stato per ogni evento dell'alfabeto.
- evento "a" = non simmetrico
Modifico soltanto il primo membro del prodotto cartesiano <x1,x3> $$ δ(x_1, a) = ND $$ Non è definita. Non faccio nulla. - evento "b" = simmetrico
Modifico entrambi i membri del prodotto cartesiano <x1,x3> $$ δ(x_1, b) = x_0 \\ δ(x_3, b) = x_4 $$ E' definita. Ottengo il prodotto cartesiano <x0,x4>. Il prodotto cartesiano non è definito. Quindi creo un nuovo stato x9=<x0,x4> e lo aggiungo a W.

- evento "c" = non simmetrico
Modifico solo il secondo membro del prodotto cartesiano <x1,x3> $$ δ(x_3, c) = x_2 $$ E' definita. Sostituisco x2 a x3 e ottengo <x1,x2>. Il prodotto cartesiano esiste già, è lo stato x6. Quindi aggiungo soltanto una transizione per "c" da x8 a x5.
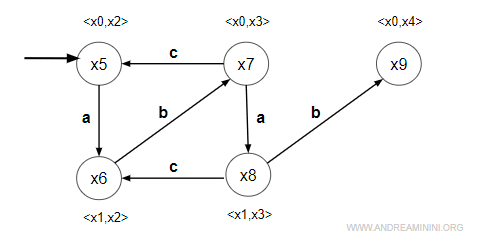
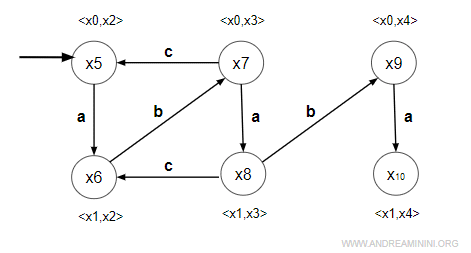
5] Analisi dello stato <x0,x4>
Prelevo uno stato da W, lo elimino da W e lo sposto in X.
$$ X = \{ x_5, x_6, x_7, x_8, x_9 \} \\ W = \{ \} $$
E' lo stato x9.
$$ x_9 = < x_0, x_4> $$
Poi analizzo le transizioni dallo stato per ogni evento dell'alfabeto.
- evento "a" = non simmetrico
Modifico soltanto il primo membro del prodotto cartesiano <x0,x4> $$ δ(x_0, a) = x_1 $$ E' definita. Il prodotto cartesiano è <x1,x4>. Non esiste ancora, quindi creo un nuovo stato X10 e lo aggiungo a W.
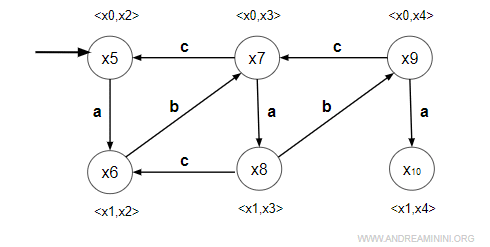
- evento "b" = simmetrico
Modifico entrambi i membri del prodotto cartesiano <x0,x4> $$ δ(x_0, b) = ND \\ δ(x_4, b) = ND $$ Non è definita. Non faccio nulla. - evento "c" = non simmetrico
Modifico solo il secondo membro del prodotto cartesiano <x0,x4> $$ δ(x_4, c) = x_3 $$ E' definita. Sostituisco x3 a x4 e ottengo <x0,x3>. Il prodotto cartesiano esiste già, è lo stato x7. Quindi aggiungo soltanto una transizione per "c" da x9 a x7.
6] Analisi dello stato <x1,x4>
Prelevo uno stato da W, lo elimino da W e lo sposto in X.
$$ X = \{ x_5, x_6, x_7, x_8, x_9, x_{10} \} \\ W = \{ \} $$
E' lo stato x10.
$$ x_{10} = < x_1, x_4> $$
Poi analizzo le transizioni dallo stato per ogni evento dell'alfabeto.
- evento "a" = non simmetrico
Modifico soltanto il primo membro del prodotto cartesiano <x1,x4> $$ δ(x_1, a) = ND $$ Non è definita. Non faccio nullo. - evento "b" = simmetrico
Modifico entrambi i membri del prodotto cartesiano <x1,x4> $$ δ(x_1, b) = x_0 \\ δ(x_4, b) = ND $$ Una transizione non è definita. Non faccio nulla. - evento "c" = non simmetrico
Modifico solo il secondo membro del prodotto cartesiano <x1,x4> $$ δ(x_4, c) = x_3 $$ E' definita. Sostituisco x3 a x4 e ottengo <x1,x3>. Il prodotto cartesiano esiste già, è lo stato x8. Quindi aggiungo soltanto una transizione per "c" da x10 a x8.
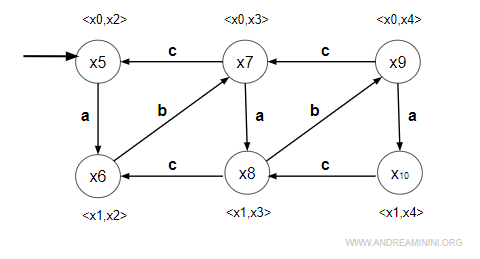
Non ci sono più stati da esplorare in W. L'algoritmo termina qui.
Ho creato la sintesi modulare dei due automi.

La sintesi è composta da 6 stati.
Nota. Il numero degli stati della sintesi è legato al numero degli stati nei moduli. Il primo automa ha n1=2 stati. Il secondo automa ha n2=3 stati. La composizione concorrente è composta da n1·n2 stati ossia 2·3=6 stati. Quindi, la cardinalità dello spazio degli stati cresce in modo esponenziale. Se avessi n moduli con k stati ciascuno, la composizione concorrente avrebbe nk stati. Questo problema è detto esplosione dello spazio degli stati. Posso evitarlo usando le reti di Petri.
E così via
