Macchina di Moore
Una macchina di Moore è un modello di automa a stati finiti deterministico (DFA) che produce un evento in uscita in funzione dello stato in cui si trova. E' definito da una 6-upla $$ G_{mo}= \{ X,E,θ,δ,λ ,x_0 \} $$
dove i parametri hanno il seguente significo
- X è l'insieme degli stati
- x0 è lo stato iniziale
- E è l'alfabeto di ingresso
- θ è l'alfabeto in uscita
- δ è la funzione di transizione da uno stato al successivo
- λ è la funzione di trasformazione ( o funzione di uscita ) λ:X→θ
La macchina prende il nome del suo ideatore Edward F. Moore.
Cosa caratterizza la macchina di Moore?
Nella macchina di Moore l'uscita (risposta) dell'automa non è determinata dagli stati in ingresso ma soltanto dallo stato corrente.
Nota. La macchina di Moore è uno dei primi dispositivi di controllo basati sul controllo logico sequenziale. Un esempio tipico di macchina di Moore è un sistema sequenziale a impulsi di clock. L'impulso di clock determina l'uscita in base allo stato corrente che in genere è salvato in un flip flop.
Come funziona
Una sequenza di eventi in ingresso e ∈ E* compone una parola
$$ w=e_1 \: e_2 \: e_3 \: ... \: e_k $$
Una parola è associata a una produzione, ossia una sequenza di stati x ∈ X
$$ x_0 \overset{e_1}{\rightarrow} x_1 \overset{e_2}{\rightarrow} x_2 \: ... \overset{e_k}{\rightarrow} x_k $$
La funzione di uscita λ(x) genera l'evento in uscita dallo stato x.
La sequenza di stati in uscita determina una parola y ∈ θ.
$$ y=λ(x_0) \: λ(x_1) \: λ(x_2) \: ... \: λ(x_k) $$
Nota. La parola in uscita è sempre più lunga della parola in entrata perché y include anche lo stato iniziale x0 dell'automa.
Nella macchina di Moore non c'è l'insieme degli stati finali Xm.
L'uscita è più generale, l'automa può trovarsi in diverse classi y ∈ θ dell'alfabeto di uscita.
Un esempio pratico
Ho un automa composto dalle classi di uscita dove V=vero, F=falso, N=nulla.
$$ θ = \{ V, F, N \} $$
Gli stati della macchina sono sei
$$ X = \{ x_0, x_1, x_2, x_3, x_4, x_5 \} $$
L'alfabeto degli eventi è composto da due simboli 0 e 1.
$$ E = \{ 0, 1 \} $$
L'automa analizza i primi due caratteri di una stringa (parola w) e risponde in uscita V,F,N se trova 11, 00 o altro.
| Stato corrente | Evento input | Stato successivo | Uscita λ(x) |
| x0 | 0 | x3 | N |
| 1 | x1 | ||
| x1 | 0 | x4 | N |
| 1 | x2 | ||
| x2 | 0 | x2 | V |
| 1 | x2 | ||
| x3 | 0 | x5 | N |
| 1 | x4 | ||
| x4 | 0 | x2 | N |
| 1 | x2 | ||
| x5 | 0 | x5 | F |
| 1 | x5 |
Il digrafo dell'automa è il seguente:
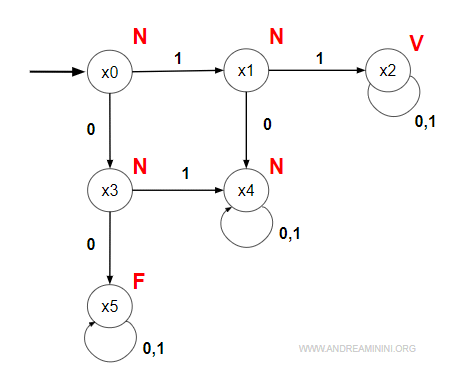
L'uscita del sistema si verifica in tre stati tramite la funzione di trasformazione λ(x):
Ad esempio, la sequenza di eventi in ingresso 1,1,0
$$ w=110 $$
genera la sequenza di stati X dell'automa
$$ x_0 \overset{1}{\rightarrow} x_1 \overset{1}{\rightarrow} x_2 \overset{0}{\rightarrow} x_2 $$
e una sequenza di uscita y
$$ y = λ(x_0) \: λ(x_1) \: λ(x_2) \: λ(x_2) = NNVV $$
Nota. La lunghezza della parola y è maggiore rispetto a quella della parola w. Confrontando l'uscita della macchina di Moore con la macchina di Mealy, si nota facilmente che la macchina di Moore è più lunga di un simbolo. E' il simbolo generato dallo stato iniziale x0 al momento dell'inizializzazione.
Come anticipato, a differenza degli altri automi a stati finiti deterministici (DFA), l'automa di Moore non ha un insieme di stati finali Xm.
Tuttavia, è comunque possibile trasformarlo in un DFA aggiungendo due classi: marcato ( finale ) e non marcato ( non finale ).
E così via.
