Macchina di Mealy
La macchina di Mealy è un automa a stati finiti deterministico (DFA) che produce un evento in funzione delle transizioni. E' una 6-upla composta da $$ G_me = \{ X, x_0, E, θ, δ, λ \} $$
- X è l'insieme degli stati
- x0 è lo stato iniziale
- E è l'alfabeto in ingresso
- θ è l'alfabeto di uscita
- δ è la funzione di transizione
- λ è la funzione di trasformazione/uscita l(x,e)
La risposta della macchina di Mealy dipende dallo stato attuale e dall'ingresso (evento) corrente.
L'automa è stato ideato nel 1955 da G.H. Mealy.
La differenza tra la macchina di Mealy e di Moore. La risposta (output) della macchina di Moore è in funzione soltanto dello stato corrente dell'automa senza prendere in considerazione gli ingressi (input).
Come funziona
Una sequenza di eventi in ingresso e ∈ E* genera una parola w
$$ w=e_1 \: e_2 \: e_3 \: ... \: e_k $$
Ogni parola w determina una produzione, ossia una sequenza di stati x ∈ X.
$$ x_0 \overset{e_1}{\rightarrow} x_1 \overset{e_2}{\rightarrow} x_2 \: ... \overset{e_k}{\rightarrow} x_k $$
L'uscita della macchina è determinata dalla funzione di trasformazione λ(x,e) in base allo stato corrente e all'evento.
La sequenza di stati in uscita determina una parola y ∈ θ.
$$ y=λ(x_0, e_1) \: λ(x_1, e_2) \: λ(x_2, e_3) \: ... \: λ(x_k-1, e_k) $$
Nota. La lunghezza della sequenza in entrata e in uscita sono uguali perché, a differenza della macchina di Moore, al momento dell'inizializzazione la macchina di Mealy non genera alcun simbolo in uscita.
Un esempio pratico
Questa macchina ha sei stati
$$ X = \{ x_0, x_1, x_2, x_3, x_4, x_5 \} $$
L'alfabeto degli eventi in ingresso è composto soltanto dai due simboli 0 e 1.
$$ E = \{ 0, 1 \} $$
L'alfabeto degli eventi in uscita è composto da V=vero, F=falso, N=nulla.
$$ θ = \{ V, F, N \} $$
L'automa analizza i primi due caratteri di una stringa in ingresso (parola w) e risponde in uscita V,F,N se trova 11, 00 o altro.
| Stato corrente (x) | Evento input (e) | Stato successivo | Uscita λ(x,e) |
| x0 | 0 | x3 | N |
| 1 | x1 | N | |
| x1 | 0 | x4 | N |
| 1 | x2 | V | |
| x2 | 0 | x2 | V |
| 1 | x2 | V | |
| x3 | 0 | x5 | F |
| 1 | x4 | N | |
| x4 | 0 | x2 | V |
| 1 | x2 | V | |
| x5 | 0 | x5 | F |
| 1 | x5 | F |
Il digrafo dell'automa è il seguente:
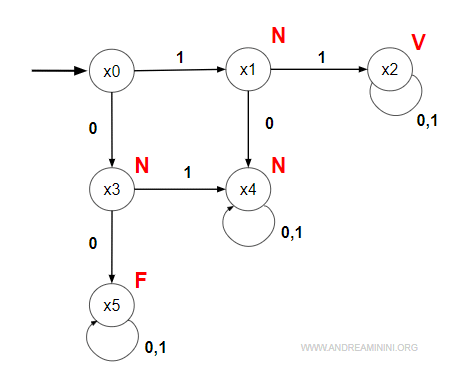
Nota. Lo stato x0 non ha un uscita perché non si è ancora verificato nessun evento. La funzione di trasformazione λ(x,e) non genera nessun output. Questo aspetto distingue la macchina di Mealy dalla macchina Moore dove, invece, anche lo stato x0 ha un uscita perché la funzione di trasformazione è basata solo sullo stato corrente λ(x).
Ad esempio, una sequenza di eventi in ingresso 1,1,0
$$ w=110 $$
genera la sequenza di stati X dell'automa
$$ x_0 \overset{1}{\rightarrow} x_1 \overset{1}{\rightarrow} x_2 \overset{0}{\rightarrow} x_2 $$
e una sequenza di uscita y
$$ y = λ(x_0,1) \: λ(x_1,1) \: λ(x_2,0) = NVV $$
E così via.
