Automa completo
Cos'è un automa completo
Un automa G a stati finiti deterministico (DFA) è detto completo se la funzione di transizione ∂(x,e) è definita per ogni stato x di X e per ogni simbolo e di E.
Se l'automa è completo, il linguaggio generato L(G) dall'automa comprende tutte le combinazioni possibili degli eventi.
$$ L(G) = E* $$
Un esempio di automa completo
Questo automa è un automa completo.
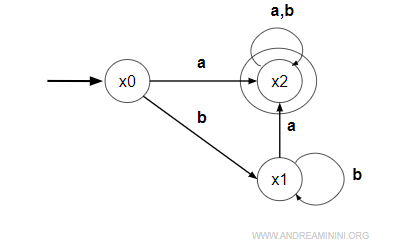
Ogni transizione possibile è definita per ogni stato X={x0,x1,x2} e simbolo E={a,b}.
$$ ∂(x_0,a)=x_2 \\ ∂(x_0,b)=x_1 \\ ∂(x_1,a)=x_2 \\ ∂(x_1,b)=x_1 \\ ∂(x_2,a)=x_2 \\ ∂(x_2,b)=x_2 $$
Un automa non completo
Un automa è non completo se almeno una transizione ∂(x,e) non è definita per uno stato e un simbolo (evento).
Esempio
Un esempio di automa incompleto.
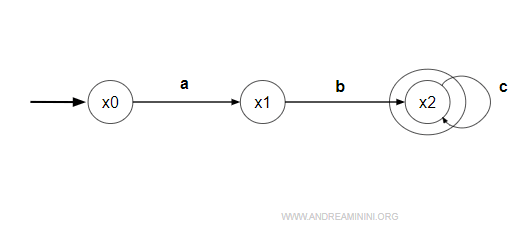
Il completamento di un automa
Un automa non completo può essere trasformato in un automa completo tramite l'operazione di completamento.
Basta aggiungere un nuovo stato xc e definire le transizioni ∂(x,e) di tutti gli eventi mancanti verso lo stato xc.
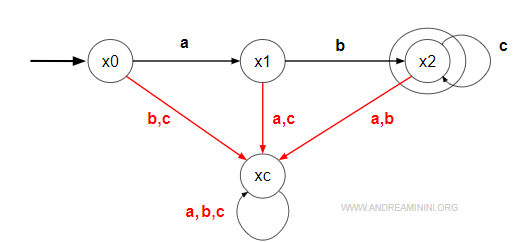
Dopo il completamento l'automa è completo, ha lo stesso stati iniziale (x0) e gli stessi stati finali (x3).
Il linguaggio dopo il completamento
L'automa completo G' ha lo stesso linguaggio accettato dell'automa incompleto.
$$ L_m(G) = L_m(G') $$
Tuttavia l'automa completo G' genera un linguaggio più ampio.
$$ L(G) ⊆ L(G') $$
Quindi sono due automi diversi dal punto di vista dinamico.
Nota. Dopo il completamento l'automa è completo ma anche bloccante, poiché lo stato xc non ha transizioni in uscita, non è uno stato finale ed è non co-raggiungibile.
E così via
