Politopo regolare

Un politopo regolare di dimensioni d è un politopo in cui tutte le facce sono figure geometriche regolari di dimensioni d-1.

Un esempio pratico

Il cubo è un politopo di 3 dimensioni.

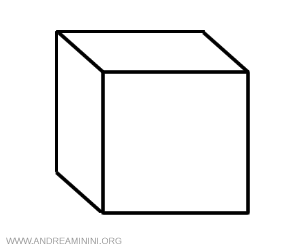
Le facce del cubo sono quadrati.

Il quadrato è un poligono regolare perché è equiangolo e equilatero.

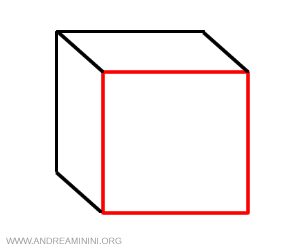
Pertanto, il cubo ha sei facce composte di politopi regolari bidimensionali (2 dimensioni).

Quindi, il cubo è un politopo regolare.

Esempio 2

Un altro esempio di politopo regolare di 3 dimensioni è il tetraedro.

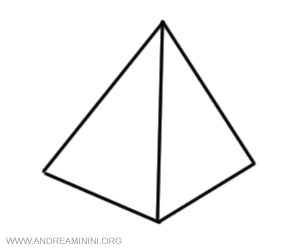
Le facce del tetraedro sono quattro triangoli equilateri.

Anche in questo caso le facce sono equiangolo ed equilatero.

Pertanto, anche il tetraedro è un politopo regolare di 3 dimensioni.

Altri esempi

Altri politopi regolari in 3 dimensioni sono l'ottaedro (8 triangoli equilateri), il dodecaedro (12 pentagoni) e l'icosaedro (20 triangoli equilateri).

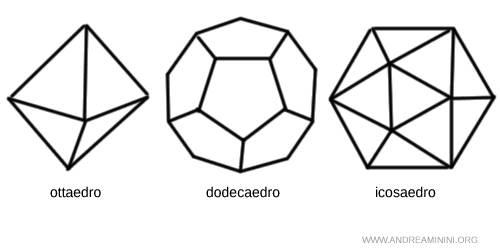
Nota. I cinque politopi regolari (cubo, tetraedro, ottaedro, dodecaedro, icosaedro) nello spazio a 3 dimensioni sono detti solidi platonici. Ognuno di questi ha come facce dei politopi bidimensionali regolari.

I politopi di 3 dimensioni sono i più semplici da comprendere perché appartengono al nostro modo di rappresentare la realtà.

Esistono però politopi regolari anche di dimensioni superiori.

I politopi regolari a n dimensioni

I politopi regolari a n dimensioni è un politopo inscrivibile in una ipersfera nello spazio Rⁿ le cui facce sono politopi regolari nello spazio R^n-1 tra loro congruenti.

Nello spazio R³ esistono cinque politopi regolari (cd solidi platonici).

Nello spazio R⁴ ci sono sei politopi regolari.

Politopi in R4	facce regolari in R3	num. facce	num. vertici
5-topo	tetraedri	5	5
8-topo	cubi	8	16
16-topo	tetraedri	16	8
24-topo	ottaedri	24	24
120-topo	dodecaedri	120	600
600-topo	tetraedri	600	120

Nello spazio R⁵ ci sono tre politopi regolari.

In ogni spazio Rⁿ di dimensione superiore (n>5) ci sono sempre tre politipi regolari.

E così via.