Politopi
Un politopo è uno spazio n-dimensionale. E' un concetto della geometria che generalizza il concetto di spazio di n dimensioni visto come un insieme limitato di punti.
E' l'analogo di un poligono nel piano (2 dimensioni) o del poliedro nello spazio ordinario tridimensionale.
Il modo migliore per capire il concetto di politopo, secondo me, è partire dai politopi elementari (una, due o tre dimensioni) e arrivare a quelli a più dimensioni.
Il politopo 1-dimensionale
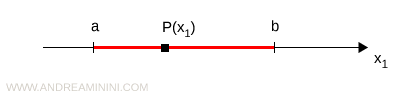
In un politopo 1-dimensionale le coordinate dei punti hanno una sola componente x1.
$$ P = (x_1) $$
Il politopo 1-dimensionale è uno spazio nell'insieme dei numeri reali R.
Pertanto, un politopo 1-dimensione è semplicemente una retta oppure un segmento.
Il politopo 2-dimensionale
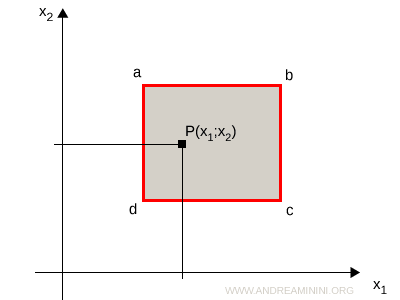
In un politopo 2-dimensionale (bidimensionale) le coordinate dei punti hanno due componenti: x1 e x2
$$ P = (x_1; x_2) $$
Il politopo 2-dimensionale è uno spazio nell'insieme dei numeri reali RxR=R2.
Quindi, il politopo 2-dimensione è un piano (x;y).
Sono politopi tridimensionali il quadrato, il rettangolo, i poligono, il cerchio, ecc.
Il politopo 3-dimensionale
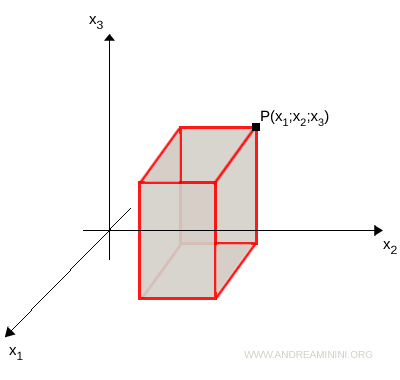
In un politopo 3-dimensionale (tridimensionale) le coordinate dei punti hanno tre componenti: x1, x2, x3.
$$ P = (x_1; x_2; x_3) $$
Il politopo 3-dimensionale è uno spazio nell'insieme dei numeri reali RxRxR=R3.
Di conseguenza, un politopo 3-dimensionale è un solido.
Sono politopi tridimensionali il cubo, il parallelepipedo, la sfera, ecc.
Nota. Fino al politopo 3-dimensionale il concetto è facilmente comprensibile perché coincide con la nostra percezione tridimensionale della realtà: punti, linee, solidi. Sono figure geometriche elementari. La difficoltà arriva quando dobbiamo immaginare politopi 4-dimensionali, 5-dimensionali o superiori.
Il politopo 4-dimensionale
In un politopo 4-dimensionale (quadridimensionale) le coordinate dei punti hanno quattro componenti: x1, x2, x3, x4.
$$ P = (x_1; x_2; x_3; x_4) $$
Il politopo 4-dimensionale è uno spazio nell'insieme dei numeri reali RxRxRxR=R4.
E' uno spazio geometrico astratto e difficile da rappresentare e da immaginare perché va oltre la nostra comune percezione tridimensionale della vita.
Tuttavia, è uno spazio geometrico esistente al pari dei precedenti.
E' composto da un insieme di punti limitato da iperpiani.
Per questa ragione lo spazio quadridimensionale è anche detto iperspazio.
Un esempio di politopo nello spazio quadridimensionale è l'ipercubo.
Esempio. Un modo semplice per immaginare un politopo 4-dimensionale è osservare un corpo in movimento nel corso del tempo. Ad esempio, un'aereo che percorre una rotta. Durante il moto l'aereo cambia le proprie coordinate (x;y;z) nello spazio tridimensionale in ogni istante di tempo t. Pertanto, l'aereo in movimento ha coordinate quadridimensionali (x;y;z;t). In fisica è un classico problema di cinematica.
Il politopo 5-dimensionale
In un politopo 5-dimensionale (pentadimensionale) le coordinate dei punti hanno cinque componenti: x1, x2, x3, x4, x5.
$$ P = (x_1; x_2; x_3; x_4; x_5) $$
Il politopo 5-dimensionale è uno spazio di punti limitato da iperpiani nell'insieme dei numeri reali R5.
E' ancora più difficile da immaginare rispetto al precedente.
Esempio. Riprendo l'esempio quadridimensionale dell'aereo in movimento. Oltre a sapere le coordinate (x;y;z) dell'aereo nel corso del tempo (t), voglio anche sapere se la pressione atmosferica (p) sulle paratie dell'aereo in ogni istante di tempo. In questo caso devo usare uno spazio 5-dimensionale perché ogni punto è caratterizzato da 5 componenti (x;y;z;t;p). E via dicendo.
Il politopo n-dimensionale
In generale un politopo n-dimensionale è un insieme limitato di punti.
Le coordinate di ogni punto hanno n-componenti.
$$ P = (x_1; x_2; x_3; x_4; ... x_n) $$
Pertanto, il politopo n-dimensionale è uno spazio nell'insieme Rn.
I politopi n-dimensionali sono molti usati nel settore del machine learning.
E così via.
