Come trovare la retta di intersezione di due piani

In questo esercizio ho le equazioni parametriche di due piani:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\ 3 \end{pmatrix} + s_1 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} + s_2 \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix} + t_1 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + t_2 \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} $$

Per trovare l'equazione della retta di intersezione tra i due piani scrivo le equazioni in un unico sistema.

$$ \begin{cases} 2+s_1 = -1+2t_1 \\ -2-s_1 -s_2 = 1-t_1 \\ 3+s_1+s_2 = 1- t_2 \end{cases} $$

Poi risolvo il sistema rispetto alle variabili s₁,s₂,t₁,t₂

$$ \begin{cases} s_1 = -3+2t_1 \\ -2-s_1 -s_2 = 1-t_1 \\ 3+(-3+2t_1)+s_2 = 1- t_2 \end{cases} $$

$$ \begin{cases} s_1 = -3+2t_1 \\ -2-s_1 -s_2 = 1-t_1 \\ 2t_1+s_2 = 1- t_2 \end{cases} $$

$$ \begin{cases} s_1 = -3+2t_1 \\ -2-s_1 -s_2 = 1-t_1 \\ s_2 = 1- t_2-2t_1 \end{cases} $$

$$ \begin{cases} s_1 = -3+2t_1 \\ -2-(-3+2t_1) -(1- t_2-2t_1) = 1-t_1 \\ s_2 = 1- t_2-2t_1 \end{cases} $$

$$ \begin{cases} s_1 = -3+2t_1 \\ t_2 = 1-t_1 \\ s_2 = 1- t_2-2t_1 \end{cases} $$

$$ \begin{cases} s_1 = -3+2(1-t_2) \\ t_1 = 1-t_2 \\ s_2 = 1- t_2-2(1-t_2) \end{cases} $$

$$ \begin{cases} s_1 = -1-2t_2 \\ t_1 = 1-t_2 \\ s_2 = t_2-1 \end{cases} $$

Quindi sostituisco s1 e s2 nella prima equazione del piano

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\ 3 \end{pmatrix} + s_1 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} + s_2 \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\ 3 \end{pmatrix} + (-1-2t_2) \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} + (t_2-1) \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\ 3 \end{pmatrix} + \begin{pmatrix} -1 \\ 1 \\ -1 \end{pmatrix} + \begin{pmatrix} -2t_2 \\ 2t_2 \\ -2t_2 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix} + \begin{pmatrix} 0 \\ -t_2 \\ t_2 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + \begin{pmatrix} -2t_2 \\ t_2 \\ -t_2 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} -2 \\ 1 \\ -1 \end{pmatrix} $$

Volendo generalizzare sostituisco il parametro t₂ con k

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} + k \begin{pmatrix} -2 \\ 1 \\ -1 \end{pmatrix} $$

Ho così trovato l'equazione parametrica della retta generata dall'intersezione dei due piani.

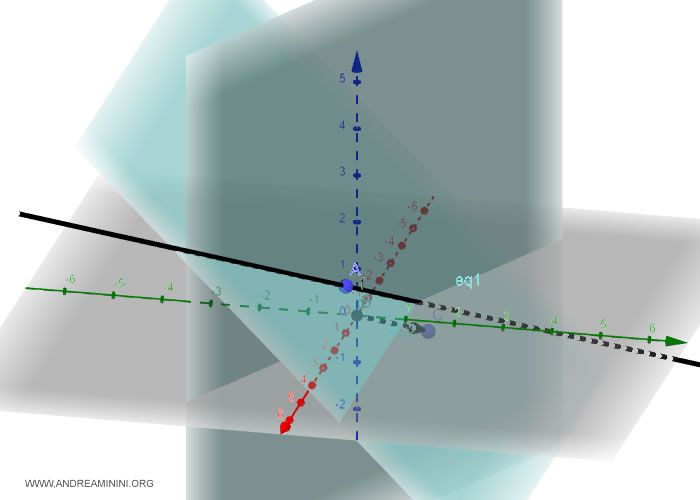
E così via.