L'accelerazione radiale e trasversa

L'accelerazione può essere rappresentata anche in forma polare . $$ a = a_r + a_θ $$ dove a_r è l'accelerazione radiale è $$ a_r = [ \frac{d^2r}{dt^2} - r ( \frac{dθ}{dt} )^2 ] \vec{u_r} $$ e a_θ è l'accelerazione trasversa $$ a_θ = [ 2 \frac{dr}{dt} \frac{dθ}{dt} + r \frac{d^2θ}{dt^2} ] \vec{u_θ} $$

Spiegazione

L'accelerazione è la derivata della velocità

$$ \vec{a} = \frac{d \vec{v}}{dt} $$

Il vettore della velocità in forma polare è composto dalla velocità radiale v_r e dalla velocità trasversa v_θ

$$ \vec{v} = \vec{v_r} + \vec{v_θ} $$

$$ \vec{v} = \frac{dr}{dt} \vec{u_r} + r \frac{dθ}{dt} \vec{u_θ} $$

Ecco la rappresentazione grafica

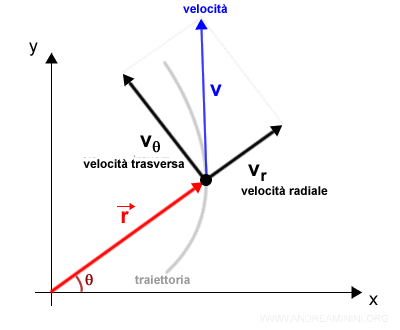
Sostituisco il vettore velocità nell'accelerazione usando la velocità radiale e trasversa

$$ \vec{a} = \frac{d \vec{v}}{dt} $$

$$ \vec{a} = \frac{d [\frac{dr}{dt} \vec{u_r} + r \frac{dθ}{dt} \vec{u_θ}]}{dt} $$

Per la proprietà lineare della derivata, la derivata di una somma è uguale alla somma delle derivate

$$ \vec{a} = \frac{d [\frac{dr}{dt} \vec{u_r} ]}{dt} + \frac{d [ r \frac{dθ}{dt} \vec{u_θ}]}{dt} $$

Applico la regola di derivazione del prodotto in entrambe le componenti

$$ \vec{a} = [ \frac{d^2r}{dt^2} \vec{u_r} + \frac{dr}{dt} \frac{d \vec{u_r}}{dt} ] + [ \frac{dr}{dt} \frac{dθ}{dt} \vec{u_θ} + r \frac{d^2θ}{dt^2} \vec{u_θ} +r \frac{dθ}{dt} \frac{ d \vec{u_θ}}{dt} ] $$

Sapendo che

$$ \frac{d \vec{u_r}}{dt} = \frac{dθ}{dt} \vec{u_θ} $$

$$ \frac{d \vec{u_θ}}{dt} =- \frac{dθ}{dt} \vec{u_r} $$

Sostituisco le componenti nell'accelerazione

$$ \vec{a} = [ \frac{d^2r}{dt^2} \vec{u_r} + \frac{dr}{dt} [ \frac{dθ}{dt} \vec{u_θ} ] ] + [ \frac{dr}{dt} \frac{dθ}{dt} \vec{u_θ} + r \frac{d^2θ}{dt^2} \vec{u_θ} + r \frac{dθ}{dt} [ - \frac{dθ}{dt} \vec{u_r} ] ] $$

$$ \vec{a} = \frac{d^2r}{dt^2} \vec{u_r} + \frac{dr}{dt} \frac{dθ}{dt} \vec{u_θ} +\frac{dr}{dt} \frac{dθ}{dt} \vec{u_θ} + r \frac{d^2θ}{dt^2} \vec{u_θ} - r ( \frac{dθ}{dt} )^2 \vec{u_r} $$

Raggruppo i termini per u_r e u_θ

$$ \vec{a} = [ \frac{d^2r}{dt^2} - r ( \frac{dθ}{dt} )^2 ] \vec{u_r} + [ 2 \frac{dr}{dt} \frac{dθ}{dt} + r \frac{d^2θ}{dt^2} ] \vec{u_θ} $$

Il primo termine è detto accelerazione radiale.

$$ a_r = [ \frac{d^2r}{dt^2} - r ( \frac{dθ}{dt} )^2 ] \vec{u_r} $$

Il secondo termine è detto accelerazione trasversa

$$ a_θ = [ 2 \frac{dr}{dt} \frac{dθ}{dt} + r \frac{d^2θ}{dt^2} ] \vec{u_θ} $$

Nota. In alcuni testi l'accelerazione trasversa è indicata nella forma equivalente contratta. $$ a_θ = [ \frac{1}{r} \frac{d [ r^2 \frac{dθ}{dt} ] }{dt} ] \vec{u_θ} $$ Basta svolgere i calcoli algebrici e differenziali per tornare alla precedente.

Pertanto, in forma polare l'accelerazione è composta dall'accelerazione radiale e dall'accelerazione trasversa.

$$ a = a_r + a_θ $$

E così via.