Le componenti cartesiane dell'accelerazione
Posso studiare l'accelerazione di un corpo tramite la proiezione del corpo sugli assi (x,y,z) del moto lungo la sua traiettoria.
$$ a = \frac{ d \: v}{d \: t } $$
Suddivido la velocità nelle sue componenti
$$ a = \frac{ d \: v_x}{d \: t } u_x + \frac{ d \: v_y}{d \: t } u_y + \frac{ d \: v_z}{d \: t } u_z $$
La derivata delle componenti della velocità è uguale alle componenti dell'accelerazione, ossia alle proiezioni dell'accelerazione sugli assi x,y,z.
$$ a = a_x u_x + a_y u_y + a_z u_z $$
Poiché $$ a_x = \frac{ d \: v_x}{d \: t } $$ $$ a_y = \frac{ d \: v_y}{d \: t } $$ $$ a_z = \frac{ d \: v_z}{d \: t } $$
L'accelerazione sul piano
L'accelerazione sul piano ha due componenti
$$ \vec{a} = \frac{d\vec{v}}{dt} $$
$$ \vec{a} = \frac{ d \: v_x}{d \: t } \vec{u_x} + \frac{ d \: v_y}{d \: t } \vec{u_y} $$
$$ \vec{a} = a_x \vec{u_x} + \vec{a_y} u_y $$
L'accelerazione può essere suddivisa anche in accelerazione tangenziale e centripeta.
$$ \vec{a} = \vec{a_T} + \vec{a_N} $$
$$ \vec{a} = \frac{ d \: v}{d \: t } \vec{u_T} + \frac{ v^2}{R} \vec{u_N} $$
Dove aT e aN sono la componente tangenziale e centripeta (o normale).
Se i versori uT e ux formano un angolo θ
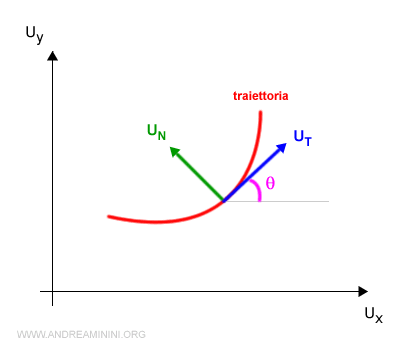
le componenti cartesiane dell'accelerazione ax e ay possono essere calcolate dalle componenti tangenziale e centripeta aT e aN tramite una rotazione del piano.
$$ a_x = \frac{d \: v}{ dt} \cos θ - \frac{v^2}{R} \sin θ $$
$$ a_y = \frac{d \: v}{ dt} \sin θ + \frac{v^2}{R} \cos θ $$
E così via.
