Campo fisica
Cosa sono i campi in fisica
Un campo in fisica è un insieme di quantità che assume una grandezza fisica in una regione dello spazio.
A seconda della natura della grandezza fisica un campo è detto
- Campo vettoriale se la grandezza fisica è una grandezza vettoriale (es. il campo elettrico, il campo magnetico, il campo gravitazionale, ecc.). I vettori sono detti linee di campo.
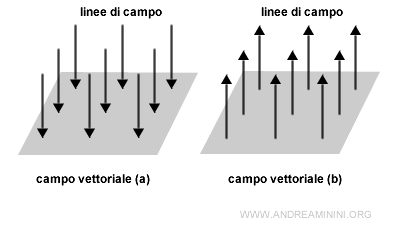
Nota. In un campo vettoriale ogni linea (vettore) è associata a un punto dello spazio. I vettori possono avere un verso in entrata sulla superficie (a) o in uscita (b) a seconda della natura della grandezza fisica. In questo esempio ho disegnato i vettori paralleli per semplicità. In realtà, possono avere anche direzione diversa tra loro.
- Campo scalare se la grandezza fisica è una grandezza scalare (es. temperatura, potenziale elettrico, ecc.). In questo caso ogni punto P dello spazio è associato a un punto di coordinate (x,y,z) e un'intensità che esprime la quantità della grandezza fisica in quel preciso punto dello spazio.
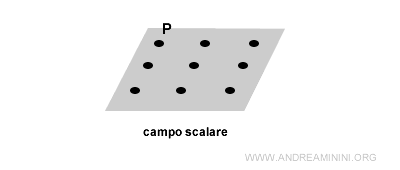
Lo spazio può essere un'area delimitata in una o due dimensioni (x,y) o un corpo definito in tre dimensioni (x,y,z).
Il campo elettrico è un esempio classico di campo vettoriale.
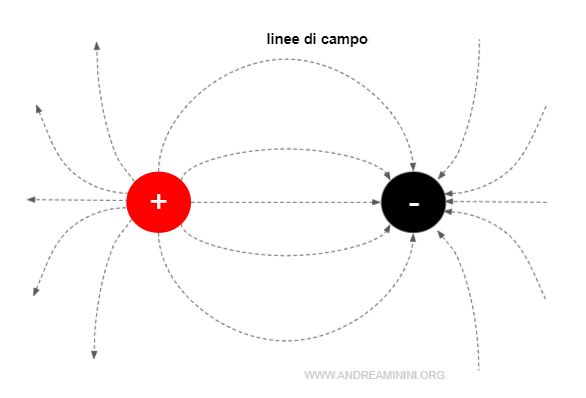
Dal punto di vista matematico un campo è una funzione che associa un vettore o un valore scalare (numero) a ogni punto dello spazio.
La funzione ha come argomento le coordinate (x,y,z) del punto
$$ φ(x,y,z) $$
oppure il vettore posizione (r) del punto
$$ φ(r) $$
In entrambi i casi la funzione associa al punto una grandezza vettoriale o scalare.
Un esempio pratico
Prendo in considerazione uno spazio delimitato S a tre dimensioni. Ad esempio, una sfera.
Ogni punto P dello spazio S è individuato dalle coordinate (x,y,z).
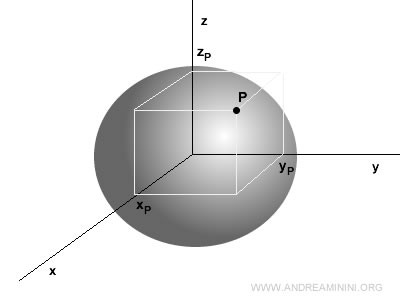
La funzione del campo associa alle coordinate P(x,y,z) una grandezza scalare o vettoriale
$$ φ(x,y,z) $$
Nel caso della sfera è però scomodo individuare i punti sulla superficie tramite le coordinate P(x,y,z).
Ogni punto P nello spazio può essere individuato anche con un vettore posizione r (o raggio vettore).
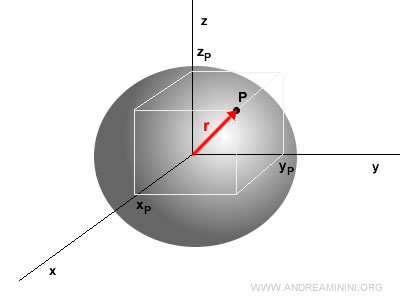
Ogni vettore posizione è caratterizzato dagli scalari x=xP, y=yP, z=zP.
$$ \vec{r} = x \cdot \vec{u}_x + y \cdot \vec{u}_y + z \cdot \vec{u}_z $$
In questo caso la funzione campo ha come argomento il vettore posizione.
$$ f(r) $$
Il risultato sempre lo stesso.
La funzione campo associa una quantità di una grandezza fisica (scalare o vettoriale) a ogni punto P dello spazio.
E così via.
