L'atomo di Bohr
Il modello atomico di Bohr venne proposto dal fisico danese Niels Bohr nel 1913 per spiegare alcune incongruenze del modello atomico di Rutherford.
Bohr fu il primo a utilizzare gli elementi fondamentali della teoria dei quanti di Max Planck per spiegare la dinamica e il comportamento dell'atomo.
Secondo Bohr, gli elettroni si muovono in orbite circolari intorno al nucleo. Queste orbite non sono però poste a caso ma seguono un ordine ben preciso.
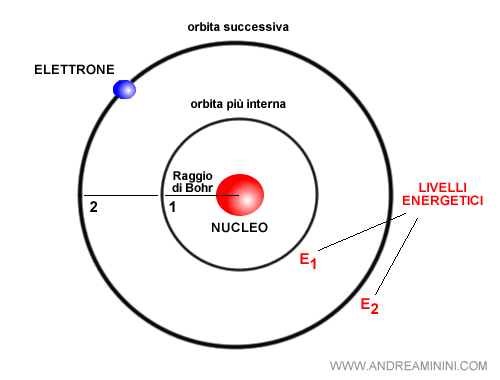
L'orbita più vicina al nucleo atomico si trova a una distanza pari a 5,2917·10-11 metri, detta raggio di Bohr.
Le orbite più esterne si trovano a distanze multiple intere del raggio di Bohr.
Pertanto, se R è il raggio di Bohr, le orbite successive si trovano a Rx2, Rx3, e così via.
A ogni orbita è associato un livello energetico. L'orbita più interna è quella con il livello energetico più basso (E1). Man mano che ci si sposta verso le orbite esterne, il livello energetico è più alto.
Il livello fondamentale. Il livello minimo di energia più vicino al nucleo atomico è detto livello fondamentale. Tutti gli altri livelli con energia superiore, invece, sono detti livelli eccitati.
Quando un elettrone passa da un'orbita esterna a quella più interna, nel salto perde una quantità di energia sotto forma di energia elettromagnetica, pari alla differenza tra i due livelli energetici delle due orbite.
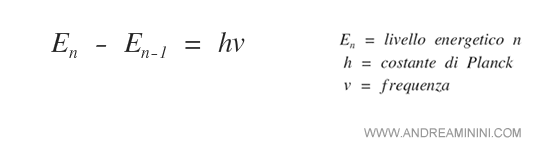
Secondo Bohr, il salto dell'orbita dell'elettrone genera un'energia En-En-1 pari all'energia del fotone.
Nota. Nella teoria dei quanti di Planck un fotone ha un'energia pari a E=hv dove h è una costante ( costante di Planck ) e v è la frequenza.
Perché gli elettroni non cadono sul nucleo atomico?
Bohr cerca di calcolare l'energia dell'elettrone nelle frequenze della serie di Balmer in cui si presentano le righe sullo spettro elettromagnetico dell'atomo di idrogeno.
Nota. L'atomo di idrogeno è formato da un solo elettrone.
Per procedere al calcolo, Bohr usa sia le leggi della fisica classica sull'elettromagnetismo che quelle della recente teoria dei quanti di Max Planck. Si tratta di un tentativo di quantizzazione delle orbite degli elettroni.
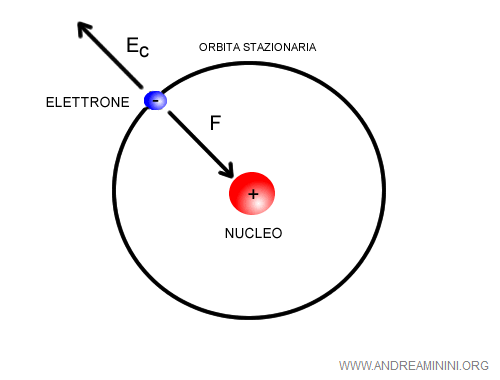
In particolar modo, secondo Bohr, per mantenere un'orbita stazionaria l'energia dell'elettrone deve essere pari alla somma tra l'energia cinetica della particella e l'energia potenziale di Coulomb ( Forza di Coulomb ).

Le due forze agiscono in direzione opposta. L'energia cinetica spinge l'elettrone verso l'esterno dell'orbita. Viceversa, l'energia potenziale coulombiana F è la forza elettromagnetica che attrae l'elettrone all'interno verso il nucleo atomico.
Sommando le due due energie otteniamo la seguente equazione:
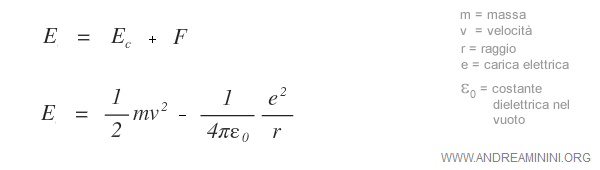
Nota. In questo caso l'energia coulombiana è negativa in quanto l'elettrone ha una carica elettrica negativa.
Per calcolare la velocità dell'elettrone, Bohr ipotizza che l'energia cinetica della forza centripeda dell'elettrone debba eguagliare la forza coulombiana che lo attrae al nucleo.
Trattandosi di una forza centripeta, la formula dell'energia cinetica deve essere sostituita con la seguente:
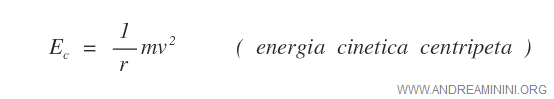
Inoltre, essendo un'interazione tra due cariche puntiformi la forza di Coulomb va riscritta nel seguente modo:
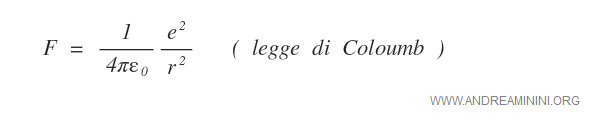
A questo punto, è sufficiente eguagliare Ec con F per trovare l'equilibrio energetico stazionario dell'elettrone.
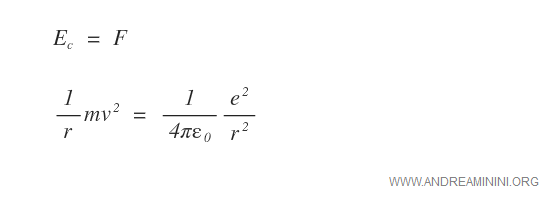
L'equazione dell'equilibrio energetico stazionario consente di mettere in evidenza mv2.
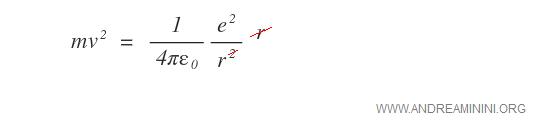
Si può così sostituire la velocità dell'elettrone mv2 in condizioni di equilibrio stazionario nell'equazione energetica iniziale dell'elettrone
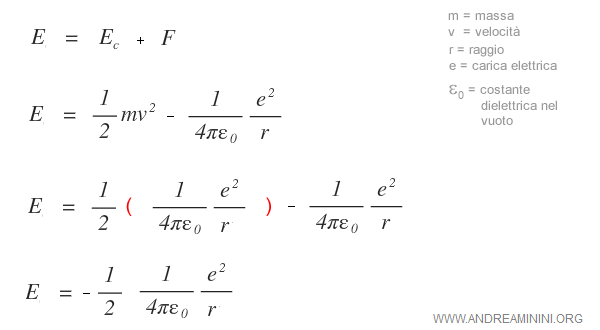
Si può affermare che, in un'orbita stazionaria l'energia cinetica Ec dell'elettrone è uguale alla metà del valore assoluto dell'energia potenziale F.
Il primo postulato di Bohr
Nel primo postulato di Bohr, il fisico afferma che l'elettrone può orbitare intorno al nucleo in modo circolare senza perdere energia, quando il raggio dell'orbita soddisfa la seguente relazione:
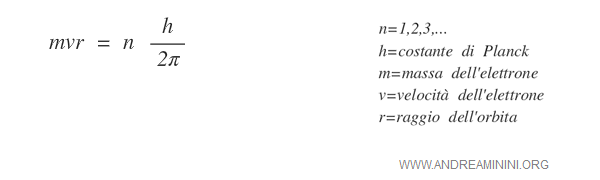
Il significato dell'equazione è il seguente: l'orbita è stazionaria quando il valore del movimento angolare ( mvr ) dell'elettrone è un multiplo intero della grandezza h/2π.
Qual è il raggio dell'orbita dell'elettrone?
L'ipotesi avanzata da Bohr nel primo postulato mi consente di calcolare esattamente il raggio dell'orbita stazionaria dell'elettrone.
In primo luogo, metto in evidenza la velocità dell'elettrone ( v )
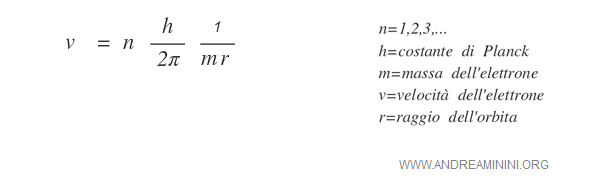
Poi sostituisco la variabile v nell'equazione dell'equilibrio energetico.

Ho così trovato l'equazione per calcolare il raggio di un'orbita n ( 1,2,3, ... ) dell'elettrone.
Nota. Nel caso dell'atomo di idrogeno, la prima orbita dell'elettrone (n=1) ha un raggio pari a 5,2917·10-11 metri.
Qual è il livello energetico dell'orbita dell'elettrone?
Una volta conosciuto il raggio dell'orbita stazionaria (n=1) posso calcolare anche il livello energetico En dell'elettrone su quell'orbita specifica.

Il secondo postulato di Bohr
Secondo il secondo postulato di Bohr, l'atomo irradia energia soltanto quando un elettrone si sposta da un'orbita stazionaria a un'altra, ossia quando effettua una transizione da uno stato stazionario iniziale a uno finale.
La frequenza della radiazione irradiata è pari alla differenza tra il livello energetico finale (Ef) e iniziale (Ei) divisi per la costante di Planck (h).
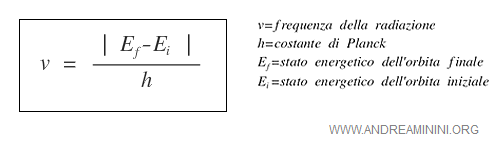
Questo postulato risolve il problema della stabilità atomica
Quando un elettrone si trova in uno stato stazionario non irradia energia. Se non perde energia... non può cadere nel nucleo.
Quanta energia elettromagnetica emette l'elettrone quando si sposta su un'orbita più interna?
Per far passare un elettrone da un'orbita esterna ( es. n=2 ) a una immediatamente più interna ( es. n=1 ), l'atomo emette una quantità di energia elettromagnetica pari alla differenza di energia dei due livelli energetici ( E1 - E2 ).
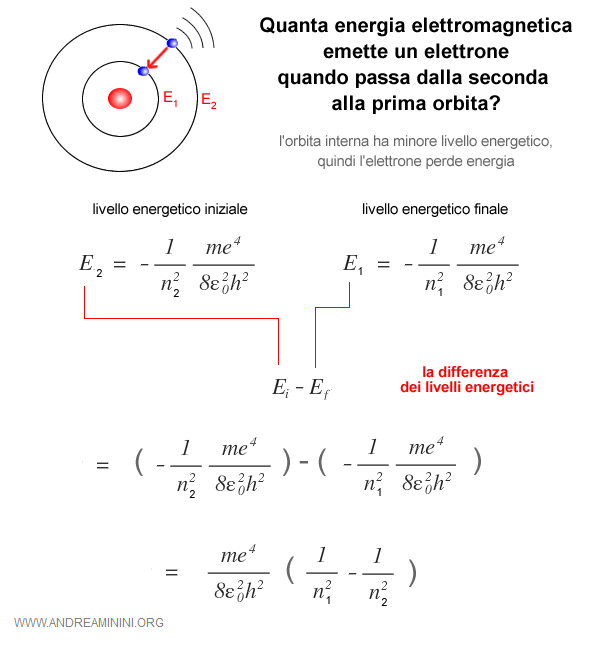
Il calcolo del raggio e del livello energetico delle orbite degli elettroni
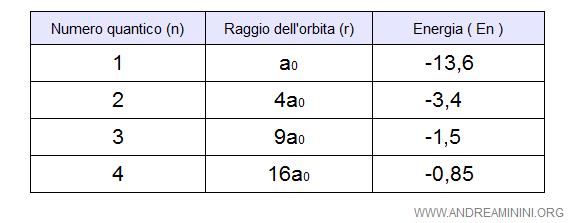
Al termine di questo lavoro posso costruire una tabella e associare a ogni numero quantico il relativo raggio dell'orbita (r) e livello energetico (En).
Nel caso dell'atomo d'idrogeno, al numero quantico n=1 ( prima orbita stazionaria ) è associato il raggio di Bohr (a0) e un livello di energia pari a -13,6 eV ( elettronvolt ). Quindi, per estrarre l'elettrone è necessario far assorbire al sistema un'energia pari a -13,6 eV.
Cosa rappresenta l'elettronvolt? L'elettronvolt ( eV ) è un'unità di misura dell'energia nella fisica atomica. In questo caso, indica l'energia cinetica dell'elettrone.
La seconda orbita stazionaria ( n=2 ) si trova, invece, a una distanza pari a 4 volte il raggio di Bohr ( 4a0 ) e un livello energetico pari a -3,4eV. E così via.
Serie di Balmer. I numeri quantici dell'atomo di Bohr equivalgolo ai numeri interi che caratterizzano la serie di Balmer. Bohr fornisce così una spiegazione alla legge empirica scritta qualche anno prima da Balmer analizzando lo spettro atomico.
