Errori a regime in un sistema a retroazione unitaria

L'analisi degli errori a regime in un sistema a retroazione permette la valutazione dell'affidabilità di un servomeccanismo.

Il sistema a retroazione unitaria

Ho un semplice sistema a retroazione con un segnale di ingresso R(t) e di uscita Y(t).

Il segnale di ingresso è un segnale di riferimento (set point).

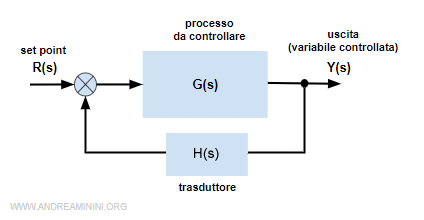
Lo scopo del sistema è di mantenere l'uscita Y(t)=R(t) e compensare gli eventuali scostamenti dovuti a cause esterne.

Quindi, è una semplice ripetizione del segnale di riferimento.

Nota. Per studiare la risposta armonica del sistema, tra le cause esterne considero vari segnali tipici. Ad esempio, un gradino, una rampa, ecc.

In questo caso il sistema ha una semplice retroazione unitaria.

$$ e(t) = R(t)-Y(t) $$

Pertanto, l'errore è semplicemente la differenza tra il segnale di riferimento R(t) e la variabile di uscita y(t) del sistema.

Se l'uscita è troppo alta Y(t)>R(t), l'errore produce automaticamente uno smorzamento, e viceversa.

La funzione di trasferimento del sistema a retroazione unitaria è

$$ Y(s) = \frac{G(s)}{1+G(s)H(s)} R(s) $$

Essendo la retroazione unitaria H(s)=1

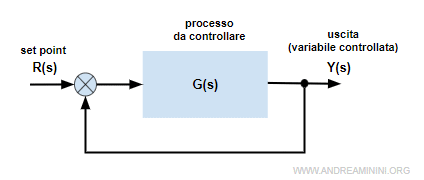
Quindi, posso semplificare la formula

$$ Y(s) = \frac{G(s)}{1+G(s)} R(s) $$

L'errore è

$$ E(s) = \frac{1}{1+G(s)} R(s) $$

Da questo punto in poi l'analisi cambia a seconda del tipo di segnale ( gradino, rampa, parabola, ecc. ) considerato.

L'analisi dell'errore a regime in risposta a un gradino

Prendo in considerazione un segnale a gradino di ampiezza A.

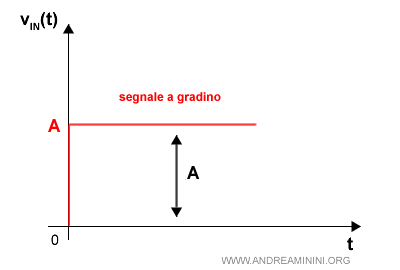
Pertanto il segnale di riferimento del sistema diventa

$$ r(t) = A \cdot u(t) $$

Calcolo la trasformata di Laplace del segnale a gradino

$$ R(s) = \frac{1}{s} A $$

Per calcolare l'errore del sistema sostituisco R(s) = A/s nella formula dell'errore E(s)

$$ E(s) = \frac{1}{1+G(s)} R(s) $$

$$ E(s) = \frac{R(s)}{1+G(s)} $$

$$ E(s) = \frac{ \frac{A}{s}}{1+G(s)} $$

L'errore a regime e_r è il comportamento asintotico dell'errore E(t) per t→∞

$$ e_r = \lim_{t \rightarrow \infty} E(t) $$

Secondo il teorema del valore finale posso riscrivere il limite in questa forma

$$ e_r = \lim_{s \rightarrow 0} s \cdot E(s) $$

Sostituisco E(s) nel limite

$$ e_r = \lim_{s \rightarrow 0} s \cdot \frac{ \frac{A}{s} }{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{A}{1+G(s)} $$

Poiché A è una costante indipendente da s

$$ e_r = \frac{A}{1+ \lim_{s \rightarrow 0} G(s)} $$

Nota. Il limite di G(s) per s→0 è detto costante di guadagno o costante di posizione. $$ K_p = \lim_{s \rightarrow 0} G(s) $$

$$ e_r = \frac{A}{1+ K_p} $$

L'errore a regime dipende dal valore della costante di posizione K_p ossia dal tipo di sistema

• Tipo 0
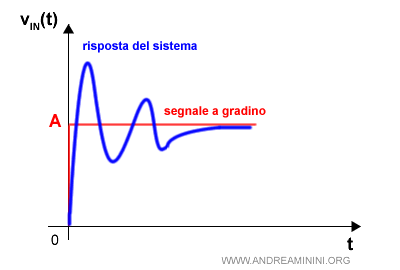
  Se la funzione G(s) non ha poli nell'origine, la costante di posizione K_p è uguale al guadagno statico.

  Nota. Nel caso del sistema di tipo 1 la costante K_p è un numero finito. Pertanto, si presenta un errore di posizione a regime. $$ e_r = \frac{A}{1+ K_p} $$ Dal punto di vista grafico la risposta al gradino è la seguente:
  

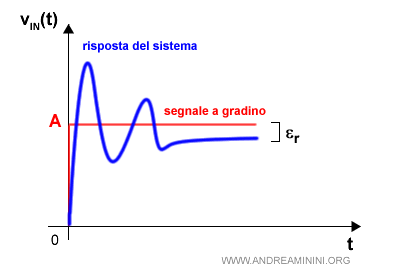
• Tipo 1
  Se la funzione G(s) ha un polo semplice nell'origine, la costante di posizione K_p=∞. Pertanto, l'errore a regime è nullo.

  Esempio
  

• Tipo 2
  Se la funzione G(s) ha due (o più) poli nell'origine, la costante di posizione K_p=∞. Anche in questo caso l'errore a regime è nullo.
  

  Nota. Nei sistemi di tipo 1 e 2 la costante di posizione è K_p=∞. Di conseguenza, l'errore a regime è nullo ossia e_r=0. $$ e_r = \frac{A}{1+ K_p} = \frac{A}{1+ ∞} = 0 $$
  

Un esempio pratico

Un sistema a retroazione unitaria ha la seguente funzione di trasferimento ad anello aperto

$$ G(s)H(s) = \frac{5}{s^2+s+2} $$

Si tratta di una funzione del tipo 0 perché non ha poli nell'origine.

Nota. Nessun valore s può annullare l'equazione di secondo grado s²+s+2.

Essendo del tipo 0, l'errore tende in modo asintotico a un valore costante.

La funzione di trasferimento ad anello chiuso è la seguente:

$$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$

Essendo a retroazione unitaria H(s)=1.

$$ W(s) = \frac{G(s)}{1+G(s)} $$

Sostituisco G(s) con la funzione fratta

$$ W(s) = \frac{\frac{5}{s^2+s+2}}{1+\frac{5}{s^2+s+2}} $$

$$ W(s) = \frac{\frac{5}{s^2+s+2}}{\frac{s^2+s+2+5}{s^2+s+2}} $$

$$ W(s) = \frac{\frac{5}{s^2+s+2}}{\frac{s^2+s+7}{s^2+s+2}} $$

$$ W(s) = \frac{5}{s^2+s+2} \cdot \frac{s^2+s+2}{s^2+s+7} $$

$$ W(s) = \frac{5}{s^2+s+7} $$

Pertanto la funzione di uscita del sistema è

$$ Y(s) = W(s) \cdot X(s) $$

$$ Y(s) = \frac{5}{s^2+s+7} \cdot X(s) $$

Applico un segnale a gradino unitario X(s)=1/s

$$ Y(s) = \frac{5}{s^2+s+7} \cdot \frac{1}{s} $$

L'errore del sistema è

$$ E(s) = \frac{1}{1+G(s)} R(s) $$

$$ E(s) = \frac{1}{1+\frac{5}{s^2+s+2}} R(s) $$

Per osservare il comportamento asintotico dell'errore per t→∞ utilizzo il teorema del valore finale

$$ \lim_{s \rightarrow 0} s \cdot E(s) $$

$$ \lim_{s \rightarrow 0} s \cdot \frac{1}{1+\frac{5}{s^2+s+2}} R(s) $$

Devo studiare la risposta a un segnale a gradino unitario R(s) = 1/s.

$$ \lim_{s \rightarrow 0} s \cdot \frac{1}{1+\frac{5}{s^2+s+2}} \frac{1}{s} $$

$$ \lim_{s \rightarrow 0} \frac{1}{1+\frac{5}{s^2+s+2}} $$

$$ \lim_{s \rightarrow 0} \frac{1}{\frac{s^2+s+2+5}{s^2+s+2}} $$

$$ \lim_{s \rightarrow 0} \frac{1}{\frac{s^2+s+7}{s^2+s+2}} $$

$$ \lim_{s \rightarrow 0} \frac{s^2+s+2}{s^2+s+7} = \frac{2}{7} $$

Pertanto, l'errore di posizione è 2/7.

$$ e_r = \frac{2}{7} = 0.28 $$

Una volta ottenuto l'errore posso calcolare l'uscita.

Essendo un gradino unitario l'uscita del sistema è

$$ Y(s) = 1 - e_r = 1 - 0.28 = 0.72 $$

Ecco il grafico della risposta del sistema

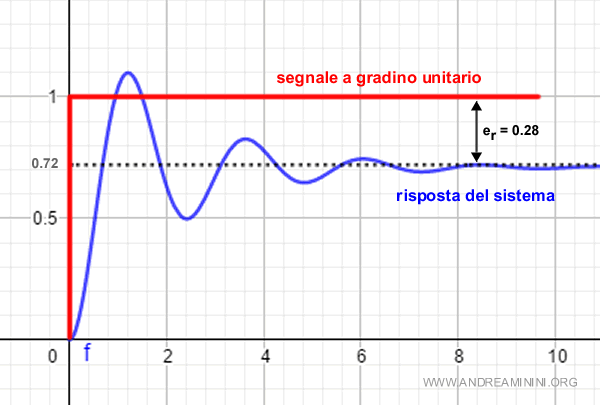
Nota. Per calcolare la formula della risposta nel dominio del tempo $$ Y(s) = \frac{5}{s^2+s+7} \cdot \frac{1}{s} $$ La risposta ha tre poli $$ p_1 = 0 $$ $$ p_2 = -0.5 + j \cdot 2.6 $$ $$ p_3 = -0.5 - j \cdot 2.6 $$ Pertanto la risposta del sistema nel tempo è $$ y(t) = 0.72 - e^{-0.5 t} \cdot [0.14 \cdot \sin(2.6 \cdot t) + 0.71 \cdot \cos(2.6 \cdot t)] $$

L'analisi dell'errore a regime in risposta alla rampa (errore di velocità)

L'errore a regime in un caso di risposta a un segnale di ingresso a rampa è diverso dal gradino.

Il segnale di ingresso a rampa con pendenza C è il seguente:

$$ r(t) = C \cdot t $$

La trasformata di Laplace del segnale è

$$ R(s) = C \cdot \frac{1}{s^2} $$

Per calcolare l'errore a regime, riprendo la formula dell'errore dopo aver applicato il teorema del valore finale.

$$ e_r = \lim_{s \rightarrow 0} \frac{sR(s)}{1+G(s)} $$

Sostituisco R(s) con la rampa

$$ e_r = \lim_{s \rightarrow 0} \frac{s\cdot [ C \frac{1}{s^2} ]}{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{C \frac{1}{s} }{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{C}{s} \frac{1}{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{C}{s+sG(s)} $$

$$ e_r = C \cdot \lim_{s \rightarrow 0} \frac{1}{s+sG(s)} $$

$$ e_r = C \cdot \frac{1}{ \lim_{s \rightarrow 0} s+ \lim_{s \rightarrow 0}sG(s)} $$

$$ e_r = C \cdot \frac{1}{ 0+ \lim_{s \rightarrow 0}sG(s)} $$

$$ e_r = \frac{C}{ \lim_{s \rightarrow 0}sG(s)} $$

Il limite di sG(s) per s→0 è detto costante di velocità.

$$ K_v = \lim_{s \rightarrow 0}sG(s) $$

Pertanto, posso riscrivere l'errore a regime in questa forma

$$ e_r = \frac{C}{ K_v } $$

Il valore della costante K dipende dal tipo di sistema e determina l'errore a regime.

• Tipo 0
  Se la funzione G(s) non ha poli nell'origine, la costante di velocità è nulla. $$ K_v = 0 $$ Quindi, l'errore a regime è infinito $$ e_r = \frac{C}{K_v} = \infty $$

  Esempio
  

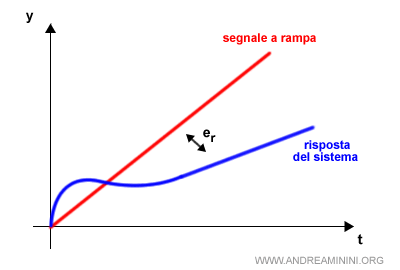
• Tipo 1
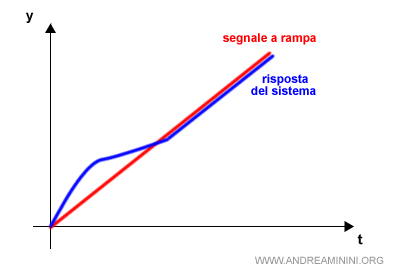
  Se la funzione G(s) ha un polo semplice nell'origine, la costante di velocità è un numero finito K. $$ K_v = K $$ Pertanto, l'errore a regime è pari a una costante C/K. $$ e_r = \frac{C}{K_v} = \frac{C}{K} $$

  Esempio. Ecco un esempio pratico di risposta con errore a regime costante.
  

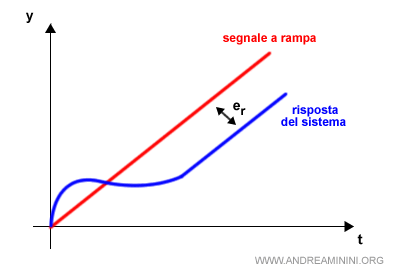
• Tipo 2
  Se la funzione G(s) ha due (o più) poli nell'origine, la costante di velocità è uguale a infinito. $$ K_v = \infty $$ In questo caso l'errore a regime è nullo. $$ e_r = \frac{C}{K_v} = \frac{C}{\infty} = 0 $$

  Esempio
  

Errore a regime in risposta alla parabola (errore di accelerazione)

L'errore a regime cambia se il segnale in ingresso è una parabola.

$$ r(t) = \frac{1}{2} C \cdot t^2 $$

La trasformata di Laplace del segnale è

$$ R(s) = \frac{C}{s^3} $$

Riprendo la formula dell'errore a regime dopo aver applicato il teorema del valore finale.

$$ e_r = \lim_{s \rightarrow 0} \frac{sR(s)}{1+G(s)} $$

Sostituisco R(s) con la parabola.

$$ e_r = \lim_{s \rightarrow 0} \frac{s[ \frac{C}{s^3} ]}{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{\frac{C}{s^2} }{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{C}{s^2} \cdot \frac{1}{1+G(s)} $$

$$ e_r = \lim_{s \rightarrow 0} \frac{C}{s^2+s^2G(s)} $$

$$ e_r = C \cdot \lim_{s \rightarrow 0} \frac{1}{s^2+s^2G(s)} $$

$$ e_r = C \cdot \frac{1}{ \lim_{s \rightarrow 0} s^2+ \lim_{s \rightarrow 0} s^2G(s)} $$

$$ e_r = C \cdot \frac{1}{ 0 + \lim_{s \rightarrow 0} s^2G(s)} $$

$$ e_r = C \cdot \frac{1}{ \lim_{s \rightarrow 0} s^2G(s)} $$

Il limite di s^2G(s) per s->0 è detto costante di accelerazione

$$ K_a = \lim_{s \rightarrow 0} s^2G(s) $$

Posso riscrivere la formula dell'errore a regime in questa forma

$$ e_r = C \cdot \frac{1}{ K_a} $$

$$ e_r = \frac{C}{ K_a} $$

La costante di accelerazione dipende dal tipo di sistema e determina l'errore a regime.

• Tipo 0
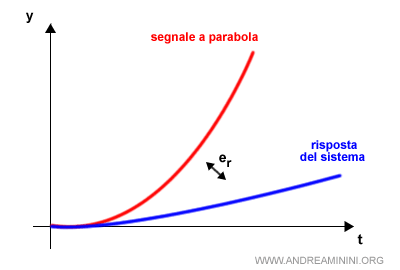
  Se la funzione G(s) non ha poli nell'origine, la costante di accelerazione è nulla $$ K_a = 0 $$ In questo caso l'errore a regime è infinito. $$ e_r = \frac{C}{K_a} = \infty $$

  Esempio
  

• Tipo 1
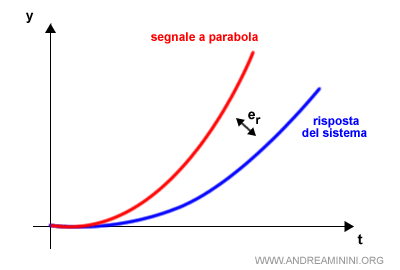
  Se la funzione G(s) ha un polo semplice nell'origine, la costante di accelerazione è nulla. $$ K_a = 0 $$ Anche in questo caso l'errore a regime è infinito. $$ e_r = \frac{C}{K_a} = \infty $$

  Esempio
  

• Tipo 2
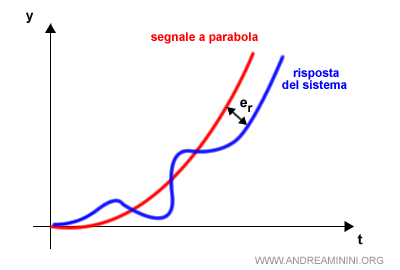
  Se la funzione G(s) ha due poli nell'origine, la costante di accelerazione è uguale a un numero finito K $$ K_a = K $$ In questo caso l'errore a regime è finito C/K. $$ e_r = \frac{C}{K_a} = \frac{C}{K} $$

  Esempio. Ecco un esempio pratico di errore a regime costante.
  

Il principio del modello interno

Per annullare l'errore a regime di un sistema in risposta a un segnale r(t) con un polo nell'origine di ordine h, devo inserire lo stesso polo nell'origine di ordine h (o superiore) nel sistema regolatore o nel sistema controllato.

Le conclusioni

Il comportamento a regime del sistema è migliore quando il tipo di sistema è elevato.

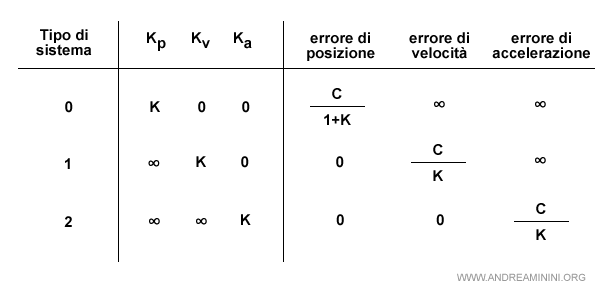
Esempio. Il comportamento dei sistemi del tipo 1, 2 o superiore è migliore rispetto al tipo 0.

Tuttavia, i sistemi di tipo 1 e 2 sono più complessi da realizzare e più instabili.

In genere, si ricorre ai sistemi di tipo 2 solo per problemi che richiedono un'elevata precisione.

E così via.