Gli approssimanti di Padé

L'approssimante di Padé permette di approssimare la funzione trascendente e^-x con una funzione razionale fratta p(x)/q(x).

L'approssimante di Padé è molto utile nello studio dei sistemi con ritardo finito

$$ F(s) = \frac{K \cdot e^{-t_0 s}}{1+Ts} $$

La funzione non razionale (trascendente) e^-t₀s può essere approssimata con una funzione razionale fratta, decisamente più facile da elaborare.

$$ e^{-t_0s} ≅ \frac{1-\frac{t_0 s}{2}+\frac{(t_0 s)^2}{12}}{1+\frac{t_0 s}{2} + \frac{(t_0 s)^2}{12}} $$

L'ordine di approssimazione di Padé

L'approssimante di Padé consiste in una funzione razionale fratta con un polinomio di ordine p al numeratore e un polinomio di ordine q al denominatore.

L'approssimante di Padé è detta approssimante di ordine (p,q)

Nota. Se p=q si dice semplicemente approssimante di ordine n con n=p=q.

Tanto più grande è l'ordine dell'approssimante, tanto più la funzione razionale fratta approssima meglio la funzione trascendente e^-t₀s.

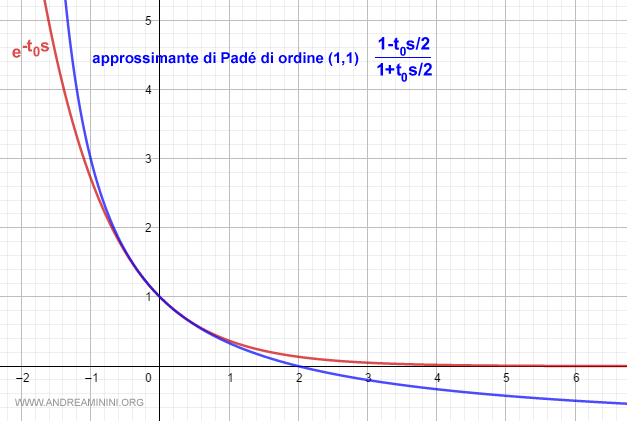
Nota. In genere si utilizza come approssimante di Padé un ordine p=q perché assicura stabilità. Anche p>q garantisce stabilità. Viceversa, un valore p<q potrebbe causare instabilità.

Esempi pratici

L'approssimante (1,1) è

$$ e^{-t_0s} ≅ \frac{1-\frac{t_0 s}{2}}{1+\frac{t_0 s}{2}} $$

L'approssimante (0,1) è

$$ e^{-t_0s} ≅ \frac{1}{1+\frac{t_0 s}{2}} $$

Nota. L'approssimazione di ordine (0,1) è molto semplice da calcolare ma può andare bene soltanto se il ritardo è molto piccolo.

L'approssimante (2,2) è

$$ e^{-t_0s} ≅ \frac{1-\frac{t_0 s}{2}+\frac{(t_0 s)^2}{12}}{1+\frac{t_0 s}{2}+\frac{(t_0 s)^2}{12}} $$

L'approssimante (3,3) è

$$ e^{-t_0s} ≅ \frac{1-\frac{t_0 s}{2}+\frac{(t_0 s)^2}{12}-\frac{(t_0 s)^3}{120}}{1+\frac{t_0 s}{2}+\frac{(t_0 s)^2}{12}+\frac{(t_0 s)^3}{120}} $$

Come costruire l'approssimante di Padé

Per costruire l'approssimante di Padé utilizzo il metodo delle potenze decrescenti

$$ e^{-s} = \frac{P(s)}{Q(s)} $$

Dove P(s) è un polinomio di ordine p

$$ P(s) = b_p s^p+b_{p-1}s^{p-1}+...+p_0 $$

e Q(s) è un polinomio di ordine q

$$ Q(s) = a_q s^q+a_{q-1}s^{q-1}+...+a_0 $$

I coefficienti a_k e b_k delle approssimanti sono determinati dai rispettivi gradi p e q dei polinomi.

$$ b_k = \frac{(p+q-k)!p!}{(p+q)!k!(p-k)!} (-1)^k \:\:\: con \: k=0,...,p $$

$$ a_k = \frac{(p+q-k)!q!}{(p+q)!k!(q-k)!} \:\:\: con \: k=0,...,q $$

Un esempio pratico

Provo a costruire l'approssimante di Padé di ordine (2,2)

Quindi il polinomio al numeratore ha ordine p=2 mentre quello al denominatore q=2.

$$ e^{-s} = \frac{P(s)}{Q(s)} = \frac{b_2 s^2+b_1s^1+b_0}{a_2 s^2+a_1s^1+a_0} $$

Calcolo i coefficienti b_k al numeratore

$$ b_k = \frac{(p+q-k)!p!}{(p+q)!k!(p-k)!} (-1)^k \:\:\: con \: k=0,...,p $$

$$ b_k = \frac{(2+2-k)!2!}{(2+2)!k!(2-k)!} (-1)^k \:\:\: con \: k=0,...,p $$

$$ b_k = \frac{(4-k)!2!}{(4)!k!(2-k)!} (-1)^k \:\:\: con \: k=0,...,p $$

$$ b_k = \frac{(4-k)!2}{24k!(2-k)!} (-1)^k \:\:\: con \: k=0,...,p $$

Quindi, per k=0

$$ b_0 = \frac{(4-0)!2}{48} (-1)^0 = 1 $$

per k=1

$$ b_1 = \frac{(4-1)!2}{24} (-1)^1 = - \frac{12}{24} = - \frac{1}{2} $$

per k=2

$$ b_2 = \frac{(4-2)!2}{96} (-1)^2 = \frac{4}{48} = \frac{1}{12} $$

Nota. Sostituisco i coefficienti b nel polinomio al numeratore. $$ e^{-s} = \frac{P(s)}{Q(s)} = \frac{b_2 s^2+b_1s^1+b_0}{a_2 s^2+a_1s^1+a_0} $$ $$ e^{-s} = \frac{P(s)}{Q(s)} = \frac{\frac{1}{12} \cdot s^2- \frac{1}{2} s^1+1}{a_2 s^2+a_1s^1+a_0} $$

Ora calcolo i coefficienti a_k al denominatore

$$ a_k = \frac{(p+q-k)!q!}{(p+q)!k!(q-k)!} \:\:\: con \: k=0,...,q $$

$$ a_k = \frac{(2+2-k)!2!}{(2+2)!k!(2-k)!} \:\:\: con \: k=0,...,2 $$

$$ a_k = \frac{(4-k)!2}{4!k!(2-k)!} \:\:\: con \: k=0,...,2 $$

$$ a_k = \frac{(4-k)!2}{24k!(2-k)!} \:\:\: con \: k=0,...,2 $$

Quindi, per k=0

$$ a_0 = \frac{(4-0)!2}{24(2-0)!} = \frac{48}{48} = 1 $$

per k=1

$$ a_1 = \frac{(4-1)!2}{24(2-1)!} = \frac{12}{24} = \frac{1}{2} $$

per k=2

$$ a_2 = \frac{(4-2)!2}{24·2·(2-2)!} = \frac{4}{48} = \frac{1}{12} $$

Nota. Sostituisco i coefficienti b nel polinomio al numeratore. $$ e^{-s} = \frac{P(s)}{Q(s)} = \frac{b_2 s^2+b_1s^1+b_0}{a_2 s^2+a_1s^1+a_0} $$ $$ e^{-s} = \frac{P(s)}{Q(s)} = \frac{b_2 s^2+b_1s^1+b_0}{\frac{1}{12} s^2+\frac{1}{2} s^1+1} $$

Una volta calcolati i coefficienti a_k e b_k posso scrivere l'approssimante di Padé di ordine (2,2).

$$ e^{-s} = \frac{P(s)}{Q(s)} = \frac{b_2 s^2+b_1s^1+b_0}{a_2 s^2+a_1s^1+a_0} $$

$$ e^{-s} = \frac{\frac{1}{12} \cdot s^2- \frac{1}{2} s^1+1}{\frac{1}{12} s^2+\frac{1}{2} s^1+1} $$

E così via.