La sensibilità alle variazioni dei parametri
La sensibilità (sensitività) è la variazione della funzione di trasferimento del sistema che si verifica dopo la variazione di un parametro (coefficiente o costante) del sistema.
La sensibilità nel sistema aperto
Prendo in considerazione un generico sistema.
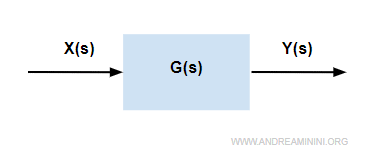
Dove la funzione di trasferimento è
$$ G(s) = \frac{Y(s)}{X(s)} $$
Quindi, l'uscita del sistema è determinata dalla seguente
$$ Y(s) = G(s)X(s) $$
La variazione di un parametro k causa una variazione dell'uscita Y(s)
$$ ΔY(s)=ΔG(s)X(s) $$
Nota. La variazione ΔG è dovuta alla variazione del parametro k dal suo valore nominale k0. $$ ΔG(s)= ( \frac{dG}{dk}|_{k=k_0} ) \cdot Δk $$
Pertanto la nuova uscita del sistema diventa
$$ Y(s) + ΔY(s) = G(s)X(s) + ΔG(s)X(s) $$
e la nuova funzione di trasferimento
$$ \frac{Y(s)+ ΔY(s)}{X(s)} = G(s)X(s) + ΔG(s)X(s) $$
Posso ricrivere il sistema come un sistema a retroazione con un blocco in parallelo.
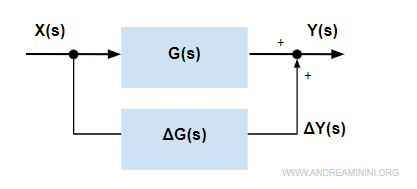
In pratica, la variazione del parametro k equivale alla presenza di un blocco indesiderato alla funzione di trasferimento.
Ecco la rappresentazione secondo le regole della riduzione in blocchi.
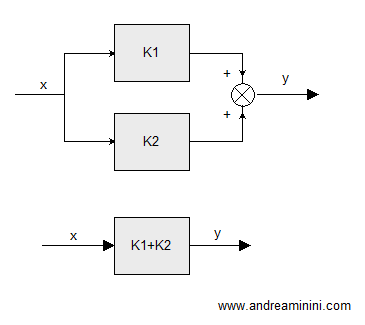
La sensibilità di un sistema a retroazione
In un sistema a retroazione la sensibilità del sistema varia a seconda del posto in cui si verifica la variazione del parametro k.
Ecco un generico sistema a retroazione negativa
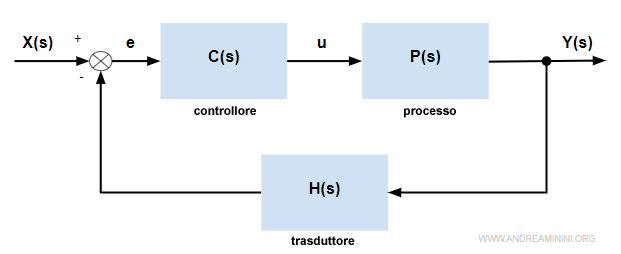
Per semplificità unisco il blocco della catena diretta in un unico simbolo G(s)=C(s)+P(s)
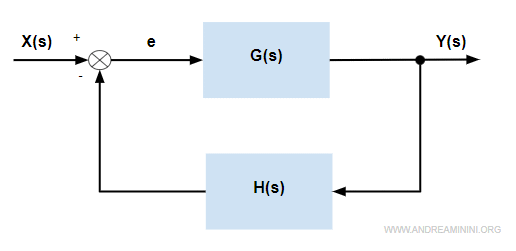
La funzione di trasferimento complessiva del sistema
$$ F(s) = \frac{Y(s)}{X(s)} $$
secondo la regola di riduzione dei blocchi dei sistemi a retroazione negativa la funzione di trasferimento diventa
$$ F(s) = \frac{G(s)}{1+G(s)H(s)} $$
La funzione G(s) al numeratore è la funzione di trasferimento diretta.
La funzione G(s)H(s) al denominatore è la funzione di trasferimento di anello.
Nota. La componente seguente è detta funzione di sensitività $$ S(s) = \frac{1}{1+G(s)H(s)} = \frac{e}{X(s)} $$
Caso 1: variazione parametro nella funzione diretta
Se la variazione si verifica nella funzione di trasferimento diretta, la variazione della funzione di trasferimento complessiva è la seguente.
$$ ΔF(s) = \frac{dF(s)}{dG(s)} \cdot \frac{dG(s)}{dk}|_{k=k_0} \cdot Δk $$
La seconda componente dell'equazione è la ΔG(s) ossia l'incremento della funzione diretta
$$ ΔF(s) = \frac{dF(s)}{dG(s)} \cdot ΔG(s) $$
Sostituisco il simbolo F(s) con la funzione di trasferimento complessiva del sistema
$$ ΔF(s) = \frac{d[ \frac{G(s)}{1+G(s)H(s)} ] }{dG(s)} \cdot ΔG(s) $$
Calcolo la derivata del rapporto rispetto a G(s)
$$ ΔF(s) = \frac{[G(s)]' \cdot (1+G(s)H(s)) - G(s) \cdot [1+G(s)H(s)]' }{[1+G(s)H(s)]^2} \cdot ΔG(s) $$
$$ ΔF(s) = \frac{1(1+G(s)H(s)) - G(s)H(s) }{[1+G(s)H(s)]^2} \cdot ΔG(s) $$
Ho così ottenuto la variazione della funzione di trasferimento complessiva
$$ ΔF(s) = \frac{1}{[1+G(s)H(s)]^2} \cdot ΔG(s) $$
La variazione relativa della funzione di trasferimento complessiva è la seguente
$$ \frac{ΔF(s)}{F(s)} = \frac{\frac{1}{[1+G(s)H(s)]^2} \cdot ΔG(s)}{ F(s) } $$
Sostituisco il simbolo F(s) con la formula
$$ \frac{ΔF(s)}{F(s)} = \frac{\frac{1}{[1+G(s)H(s)]^2} \cdot ΔG(s)}{ \frac{G(s)}{1+G(s)H(s)} } $$
$$ \frac{ΔF(s)}{F(s)} = \frac{1}{[1+G(s)H(s)]^2} \cdot ΔG(s) \cdot \frac{1+G(s)H(s)}{G(s)} $$
$$ \frac{ΔF(s)}{F(s)} = \frac{1}{1+G(s)H(s)} \cdot ΔG(s) \cdot \frac{1}{G(s)} $$
$$ \frac{ΔF(s)}{F(s)} = \frac{1}{1+G(s)H(s)} \cdot \frac{ΔG(s)}{G(s)} $$
Nota. Il primo fattore è la funzione di sensitività S(s). $$ \frac{ΔF(s)}{F(s)} = S(s) \cdot \frac{ΔG(s)}{G(s)} $$
Utilizzo la precedente in una funzione di risposta armonica, ossia in una funzione di variabile complessa
$$ \frac{ΔF(jω)}{F(jω)} = \frac{1}{1+G(jω)H(jω)} \cdot \frac{ΔG(jω)}{G(jω)} $$
I rispettivi modulo sono
$$ \frac{|ΔF(jω)|}{|F(jω)|} = \frac{1}{|1+G(jω)H(jω)|} \cdot \frac{|ΔG(jω)|}{|G(jω)|} $$
Se le pulsazioni sono tali che |G(jω)H(jω)|>>1 la sensitività S(s)>1
$$ \frac{ΔF(jω)}{F(jω)} << \frac{ΔG(jω)}{G(jω)} $$
In conclusione, se le frequenze ω generano un guadagno di anello molto alto, l'errore relativo a un parametro della funzione diretta G(s) è molto inferiore in un sistema a retroazione rispetto a un sistema ad anello aperto.
Caso 2: variazione parametro nella funzione ad anello
Se la variazione si verifica nella funzione di trasferimento ad anello del trasduttore, la variazione della funzione di trasferimento complessiva è la seguente.
$$ ΔF(s) = \frac{dF(s)}{dH(s)} \cdot \frac{dH(s)}{dk}|_{k=k_0} \cdot Δk $$
L'ultima componente è l'incremento di ΔH(s) ossia del blocco del trasduttore
$$ ΔF(s) = \frac{dF(s)}{dH(s)} \cdot ΔH(s) $$
Sostituisco il simbolo F(s) con la funzione di trasferimento complessiva del sistema
$$ ΔF(s) = \frac{d[ \frac{G(s)}{1+G(s)H(s)} ]}{dH(s)} \cdot ΔH(s) $$
Calcolo la derivata del rapporto rispetto a H(s) e ottengo la variazione relativa della funzione di trasferimento complessiva
$$ ΔF(s) = \frac{0 - G(s) G(s)}{[1+G(s)H(s)]^2} \cdot ΔH(s) $$
$$ ΔF(s) = \frac{- G^2(s)}{[1+G(s)H(s)]^2} \cdot ΔH(s) $$
La variazione relativa della funzione di trasferimento complessiva è, invece, la seguente
$$ \frac{ΔF(s)}{F(s)} = \frac{ \frac{- G^2(s)}{[1+G(s)H(s)]^2} \cdot ΔH(s) }{ \frac{G(s)}{1+G(s)H(s)} } $$
$$ \frac{ΔF(s)}{F(s)} = \frac{- G^2(s)}{[1+G(s)H(s)]^2} \cdot ΔH(s) \cdot \frac{1+G(s)H(s)}{G(s)} $$
$$ \frac{ΔF(s)}{F(s)} = \frac{- G^2(s)}{1+G(s)H(s)} \cdot \frac{ΔH(s) }{G(s)} $$
$$ \frac{ΔF(s)}{F(s)} = \frac{- G(s)}{1+G(s)H(s)} \cdot ΔH(s) $$
In questo caso gli errori sono dello stesso ordine di grandezza.
E così via.
