Sistema in forma minima

Cos'è un sistema in forma minima

Un sistema in forma minima è un modello matematico che sintetizza in un unico blocco tutti i sottomodelli matematici, gli ingressi e le uscite del sistema.

Metodi per ridurre un sistema in forma minima

Per ridurre un sistema in forma minima posso usare tre metodi:

• Metodo algebrico
• Regole di riduzione elementari
• Formula di Maison

Metodo di riduzione algebrico

La riduzione del sistema in forma minima con il metodo algebrico consiste in questi passi:

1. Creo delle variabili intermedie (p)
2. Scrivo le combinazioni lineari di ogni variabile intermedia (p) e di uscita (y)
3. Semplifico le variabili intermedie per sostituzione
4. Risolvo le equazioni per trovare y come combinazione lineare della variabile di ingresso x

Nota. Non si tratta di un metodo algoritmico. Pertanto, la scelta delle variabili intermedie e delle semplificazioni algebriche per arrivare a y=∝x è arbitraria. Per arrivare alla stessa soluzione ci sono diverse strade tra cui scegliere.

Esempio

Devo ridurre in forma minima questo sistema.

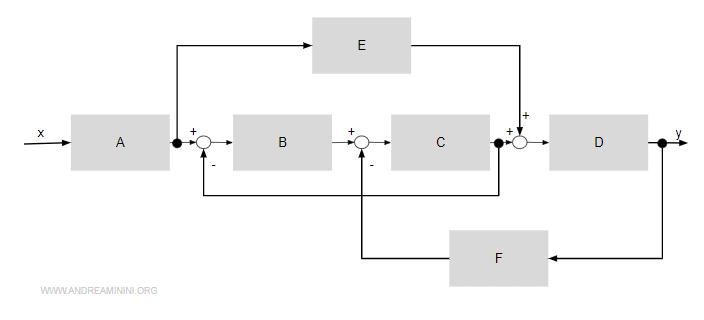
Creo tre variabili intermedie in corrispondenza delle uscite dei sommatori.

Le chiamo P1, P2, P3.

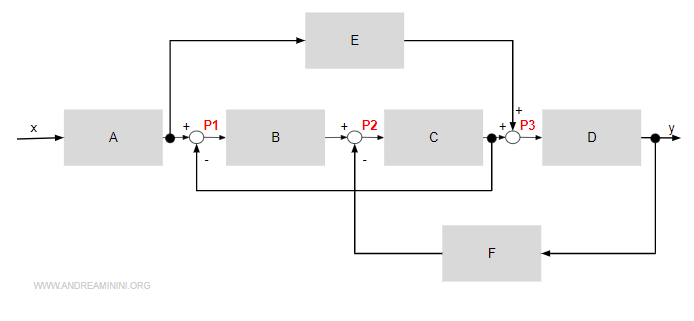
Ogni punto P identifica l'ingresso di un blocco intermedio.

Questo mi permette di calcolare l'equazione algebrica di ogni variabile intermedia.

$$ P_1 = A \cdot x-C \cdot P_2$$

$$ P_2 = B \cdot P_1 -F (D \cdot P_3) $$

$$ P_3 = E ( A \cdot x ) +C \cdot P_2 $$

Ogni blocco è moltiplicato per la sua variabile in ingresso ( ad esempio A per x ).

In questo modo, ogni variabile P_n è una combinazione lineare di altre variabili.

Nota. Nella seconda equazione ho scritto FDP3 anziché Fy. E' necessario farlo perché y è la variabile dipendente del sstema. Per usare il segnale in uscita di F devo indicare il blocco F moltiplicato per il suo ingresso P3. E' una forma equivalente di y.

Ora posso calcolare l'equazione algebrica di ogni uscita del sistema per sostituzione.

In questo caso c'è solo un'uscita y.

$$ y= p_3 \cdot D $$

Risolvo l'equazione precedente per sostituzione.

Devo fare in modo che P₃ contenga anche P₁ e P₂.

Prima sostituisco P₁ in P₂.

$$ P_2 = BP_1 -FDP_3 $$

$$ P_2 = B(Ax-CP_2) -FDP_3 $$

$$ P_2 = BAx-BCP_2 -FDP_3 $$

$$ P_2 + BCP_2 = BAx -FDP_3 $$

$$ P_2 (1+ BC) = BAx -FDP_3 $$

$$ P_2 = \frac{1}{(1+ BC) } \cdot ( BAx -FDP_3 ) $$

Poi sostituisco P2 in P3.

$$ P_3 = EAx +CP_2 $$

$$ P_3 = EAx +C ( \frac{1}{1+ BC } \cdot ( BAx -FDP_3 ) ) $$

$$ P_3 = \frac{(1+BC)EAx +CBAx-CFDP_3}{1+ BC } $$

$$ P_3 + \frac{CFDP_3}{1+ BC} = \frac{(1+BC)EAx +CBAx}{(+ BC } $$

$$ \frac{(1+BC)P_3 +CFDP_3}{1+ BC} = \frac{(1+BC)EAx +CBAx}{1+ BC } $$

$$ \frac{P_3(1+BC+CFD)}{1+ BC} = \frac{(1+BC)EAx +CBAx}{1+ BC } $$

$$ P_3(1+BC+CFD) = (1+BC)EAx +CBAx $$

$$ P_3 = \frac{(1+BC)EAx +CBAx}{1+BC+CFD} $$

Infine,sostituisco P₃ nell'equazione y.

$$ y= P_3 \cdot D $$

$$ y= \frac{(1+BC)EAx +CBAx}{1+BC+CFD} \cdot D $$

$$ y= \frac{(1+BC)EADx +CBADx}{1+BC+CFD} $$

$$ y= \begin{pmatrix} \frac{(1+BC)EAD +CBAD}{1+BC+CFD} \end{pmatrix} \cdot x $$

$$ y= \begin{pmatrix} \frac{D[(1+BC)EA +CBA]}{1+BC+CFD} \end{pmatrix} \cdot x $$

$$ y= \begin{pmatrix} \frac{D(EA+EABC +CBA)}{1+BC+CFD} \end{pmatrix} \cdot x $$

$$ y= \begin{pmatrix} \frac{AD(E+EBC +CB)}{1+BC+CFD} \end{pmatrix} \cdot x $$

Ho così trovato il modello matematico del sistema in forma minima.

Dove y è una combinazione y=αx.

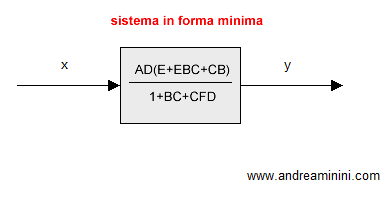
Ora nello schema c'è un unico blocco con un ingresso x e un'uscita y.

Metodo delle regole elementari

Posso ridurre un sistema in forma minima anche usando le regole elementari di riduzione dello schema a blocchi.

Un esempio pratico

Riprendo il sistema precedente.

Sposto il sommatore tra B e C a monte di B.

Questo spostamento trasforma il contenuto del blocco F a F/B.

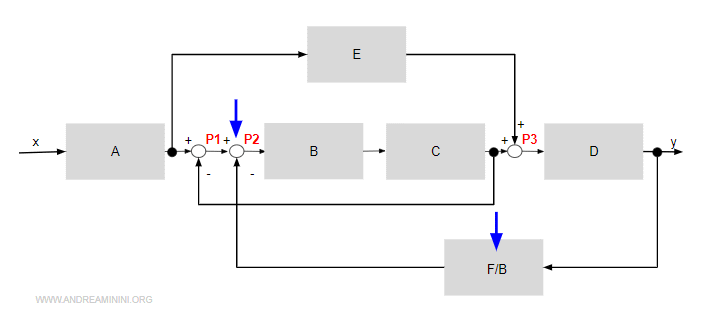
Ora i blocchi B e C sono in cascata.

Quindi posso unirli in un unico blocco BC

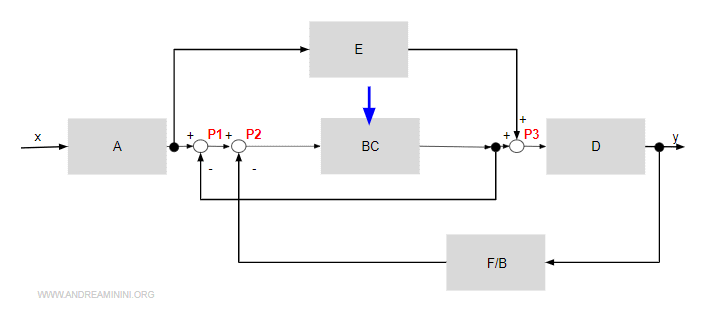
Sposto il sommatore P2 prima di P1.

Questa modifica non comporta variazioni.

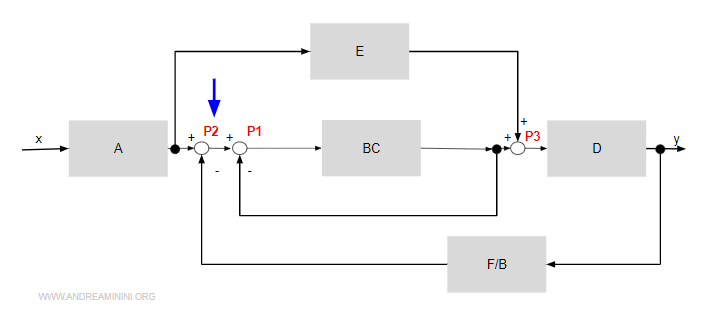
A questo punto applico la regola per eliminare l'anello con retroazione negativa intorno a BC.

Nell'anello non c'è nessun blocco. Quindi vale 1.

Il guadagno dell'anello BC diventa BC/(1+BC).

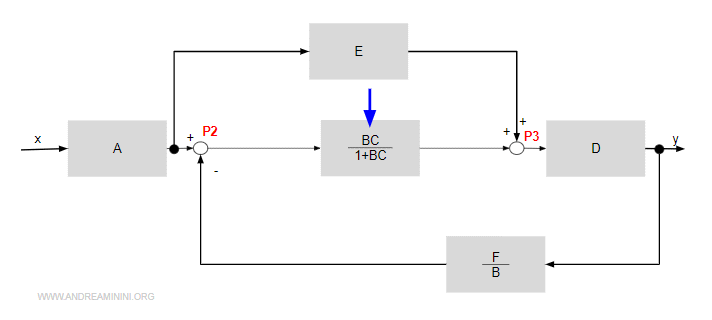
Attenzione. La regola per sostituire un anello cambia a seconda se la retroazione è positiva o negativa. A volte i manuali dimenticano di specificarlo.

Poi sposto il sommatore P3 a sinistra del blocco BC/1+BC.

Il blocco E diventa E(1+BC)/BC.

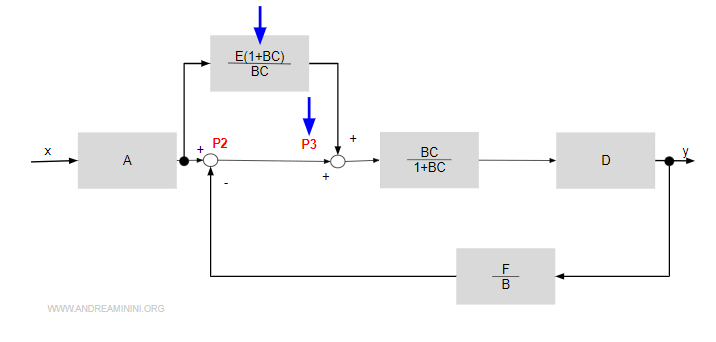
A questo punto unisco i due blocchi in cascata BC/(1+BC) e D.

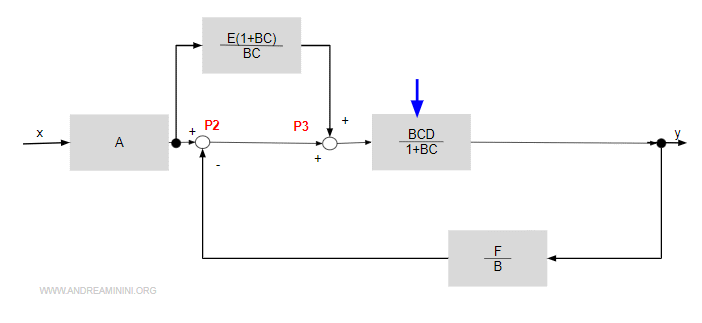
Poi sposto il puntatore P2 a destra di P3.

In questo modo si crea un parallelo e una retroazione negativa.

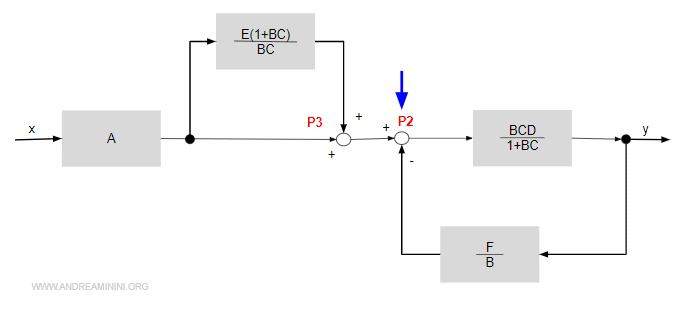
Applico la regola di semplificazione del parallelo a sinistra di P3.

Il nuovo blocco è la somma di 1 (collegamento senza blocco) e E(1+BC)/BC.

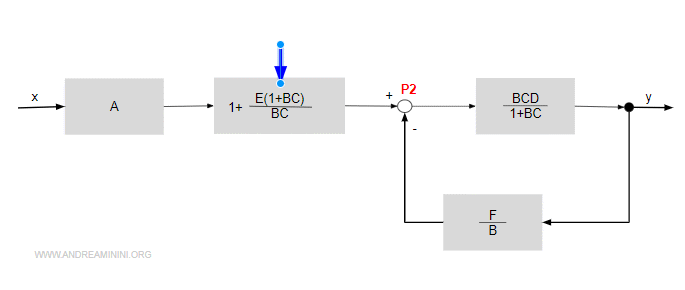
Ora elimino la retroazione negativa a destra.

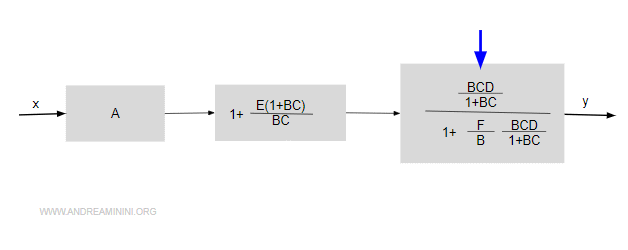
Effettuo qualche semplificazione algebrica.

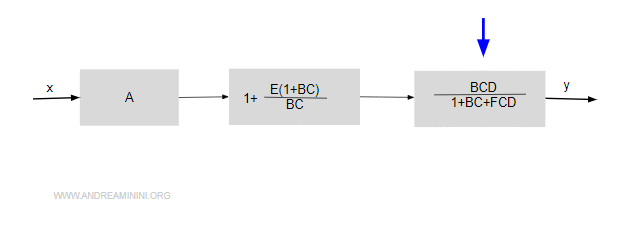
Infine, applico la regola per unire i tre blocchi in cascata.

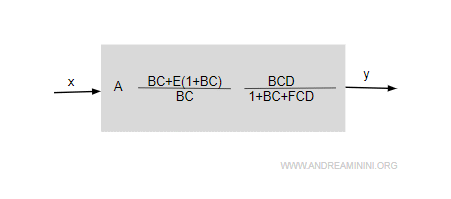
Il guadagno può essere ulteriormente semplificato.

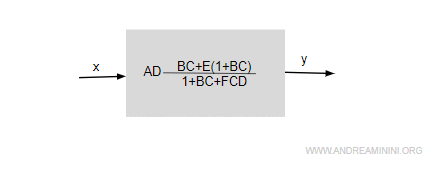
Ho così trovato il sistema in forma minima.

E' lo stesso trovato con il metodo algebrico.

E così via.