Modello ISU

Cos'è il modello ISU

Nella teoria dei sistemi un modello ISU di un sistema è un modello composto dagli ingressi (I), dallo stato (S) e dalle uscite (U).

Come costruire un modello ISU

Per trovare il modello matematico di un modello ISU scrivo le equazioni del fenomeno da studiare.

In genere si tratta di equazioni differenziali nella seguente forma generale.

$$ f(y^n,y^{n-1},...,u^m,...,u)=0 $$

Nel caso del modello ISU c'è anche una terza variabile di stato (x) oltre alle variabili di ingresso (u) e di uscita (y).

Osservando le equazioni indivduo le variabili in ingresso secondo il principio di causalità.

Nota. Secondo il principio di causalità le variabili di ingresso (u) sono quelle derivate il minor numero di volte nelle equazioni differenziali.

Poi individuo l'ordine del sistema, ossia il massimo grado di derivazione.

L'ordine del sistema determina il numero delle variabili di stato.

Infine, riscrivo il sistema differenziando ogni n-esima variabile di stato (x) rispetto al tempo

$$ \dot{x_1} = f_1(x_1,...,x_n,u_1,...,u_m, t) \\ \vdots \\ \dot{x_n} = f_n(x_1,...,x_n,u_1,...,u_m, t) $$

con m variabili di ingresso (u) e una variabile tempo.

Poi differenzio ogni p-esima uscita (y) del sistema rispetto al tempo

$$ \dot{y_1} = g_1(x_1,...,x_n,u_1,...,u_m, t) \\ \vdots \\ \dot{y_p} = g_p(x_1,...,x_n,u_1,...,u_m, t) $$

con m variabili di ingresso (u) e una variabile tempo.

Nota. Non occorre che siano presenti tutte. Al più potrebbero esserci queste variabili. Spesso ne servono soltanto alcune.

Un esempio pratico

Ho un circuito elettrico RLC

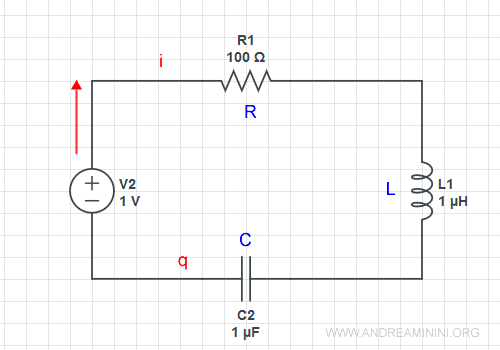
Il sistema di equazioni del circuito elettrico è

$$ \begin{cases} e=Ri-L\dot{i}+\frac{q}{C} \\ i=\dot{q} \end{cases} $$

Nota. Essendo la corrente uguale alla derivata della carica elettrica i=D[q]. Quindi potrei ridurre il sistema a due sole variabili. $$ \begin{cases} e=R\dot{q}-L\ddot{q}+\frac{q}{C} \\ i=\dot{q} \\ \dot{i}=\ddot{q} \end{cases} $$ Tuttavia, per agevolare la spiegazione in questo esempio preferisco lasciare tutte le variabili espresse con il loro nome.

Le variabili del sistema sono tre

$$ e,i,q $$

La variabile e (forza elettromotrice) è derivata zero volte. Le variabili i (corrente) e q (carica elettrica) sono derivate una volta.

Quindi, la forza elettromotrice (e) è l'unica variabile di ingresso (u) del sistema, essendo derivata meno volte.

$$ u=q $$

Le variabili i e q sono potenziali variabili di uscita (y).

Nota. Sono "potenziali" variabili di uscita perché potrei scegliere una, l'altra o entrambe a seconda del problema che devo risolvere.

L'ordine del sistema (n) è uguale alla somma delle derivazioni nelle variabili di uscita.

Quindi, l'ordine n del sistema è uguale a 2.

$$ n = 2 $$

Nota. Le variabili di uscita i,q sono derivate una volta. Quindi, n=1+1=2.

Il numero delle variabili di stato (x) coincide con l'ordine (n) del sistema.

$$ x_1=q \\ x_2=i $$

A questo punto scrivo le equazioni delle variabili di stato differenziate rispetto al tempo.

$$ \dot{x_1} = f_1(x_1,x_2,u) $$

$$ \dot{x_2} = f_2(x_1,x_2,u) $$

Nota. Non è detto che debbano essere in funzione di x1,x2,u bensì al più di x1,x2 e u.

Di sicuro, non possono essere in funzione di altre variabile. Se dovesse accadere, c'è qualcosa di errato nel modello.

Sapendo che x1=q

$$ \dot{x_1} = f_1(x_1,x_2,u) = \dot{q} = i = x_2 $$

Sapendo che x2=i

$$ \dot{x_2} = f_1(x_1,x_2,u) = \dot{i} = \frac{1}{L}e - \frac{R}{L}i - \frac{1}{LC}q $$

Sapendo che e=u, i=x1, q=x2

$$ \dot{x_2} = f_1(x_1,x_2,u) = \dot{i} = \frac{1}{L}e - \frac{R}{L}i - \frac{1}{LC}q = \frac{1}{L}u - \frac{R}{L}x_2 - \frac{1}{LC}x_1 $$

Infine, differenzio le variabili di uscita y1 e y2 del sistema rispetto al tempo.

$$ y_1 = g_1(x_1,x_2,u) $$

$$ y_2 = g_2(x_1,x_2,u) $$

In questo caso y1=i che a sua volta è uguale a x2.

$$ y_1 = g_1(x_1,x_2,u) = i = x_2 $$

E y2=q che a sua volta è uguale a x1.

$$ y_2 = g_2(x_1,x_2,u) = q = x_1 $$

In conclusione, le equazioni del modello ISU sono le seguenti

$$ \begin{cases} \dot{x_1} = x_2 \\ \dot{x_2} = \frac{1}{L}u - \frac{R}{L}x_2 - \frac{1}{LC}x_1 \\ y_1 = x_2 \\ y_2 = x_1 \end{cases} $$

Ho trovato le equazioni del modello ISU.

E così via.