Diagrammi polari di Nyquist
Cosa sono i diagrammi polari
I diagrammi polari (o diagrammi di Nyquist) sono una forma di rappresentazione di una funzione di risposta armonica sul piano di Gauss.
Sono uno strumento alternativo ai diagrammi di Bode.
Nota. Il diagramma di Nyquist ha il vantaggio d'essere più sintetico rispetto al diagramma di Bode. Ha però lo svantaggio di non descrivere l'andamento della funzione quando il modulo assume valori molto piccoli, poiché è un diagramma non logaritmico.
Come funziona il diagramma di Nyquist
Il diagramma polare mostra la variazione del numero complesso G(jω) sul piano di Gauss in funzione della pulsazione ω.
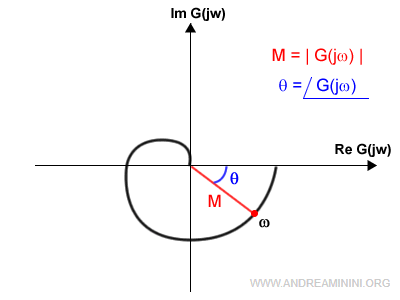
Ogni pulsazione ω individua un punto del piano in cui M è il modulo di G(jω) e la fase θ è l'argomento di G(jω).
Come disegnare il diagramma polare
Un primo modo per tracciare il diagramma polare è rilevare i valori della parte reale e della parte immaginaria del numero complesso per diverse pulsazioni ω.
Si tratta però di un processo lungo. Inoltre, non saprei quali pulsazioni scegliere piuttosto che altre.
E' preferibile tracciare un diagramma approssimativo seguendo alcune regole pratiche
Posso tracciare il diagramma di Nyquist prendendo in considerazione solo le pulsazioni w di (0,+∞). Il tacciamento dell'intervallo (-∞,0) è simmetrico.
Prendo in considerazione la funzione di trasferimento in forma fattorizzata
$$ G(s) = K \cdot \frac{ (1+τ'_1s) (1+τ'_2s) ... (1+2δ'_1 \frac{s}{ω'_{n1}} + \frac{s^2}{ω'^2_{n1}} ) (1+2δ'_2 \frac{s}{ω'_{n2}} + \frac{s^2}{ω'^2_{n2}} ) }{ s^h ( 1+τ_1s ) ( 1+τ_2s ) ... ( 1+2δ_1 \frac{s}{ω_{n1} } + \frac{s^2}{ω^2_{n1}} ) ( 1+2δ_2\frac{s}{ω_{n2}} + \frac{s^2}{ω^2_{n2}} ) } $$
Nota. Posso usare anche la funzione di trasferimento in questa forma ma le regole sono leggermente diverse. $$ G(s) = K_1 \cdot \frac{ s^m + b_{m-1}s^{m-1}+...+_1s+b_0 }{ s^h (s^{n-h}+a_{n-1}s^{n-h-1}+...+a_{h+1}s+a_h } $$
La variabile h è il numero del poli nell'origine.
1] Comportamento per ω → 0+
Analizzo il comportamento della funzione di trasferimento quando le pulsazioni ω tendono a zero da destra.
$$ \lim_{ω \rightarrow 0^+} G(jω) $$
Possono verificarsi due casi
Caso 1 (h=0)
Se il valore h=0 nella funzione, allora il diagramma parte da un punto K dell'asse reale.
$$ \lim_{ω \rightarrow 0^+} G(jω) = K $$
con una fase pari a
$$ φ(0)=arg(K)=\begin{cases} 0° \:\:\: se \: K>0 \\ \\ ±180° \:\:\: se \: K<0 \end{cases} $$
Nota. Se sto usando la funzione di trasferimento in forma non fattorizzatata $$ \lim_{ω \rightarrow 0^+} G(jω) = K_1 \frac{b_0}{a_0} $$
In questo caso il diagramma comincia da un punto (K,0) del piano di Gauss.
Esempio. In una funzione di trasferimento a un polo e nessuno zero al numeratore. $$ G(jω) = K \cdot \frac{1}{(1+jωτ_1)} $$ per ω=0 vale K con una fase φ(0)=0° ossia un angolo di 0° . $$ G(jω) = K \cdot \frac{1}{(1+j(0)τ_1)} = K $$ Ho così individuato il punto di partenza.
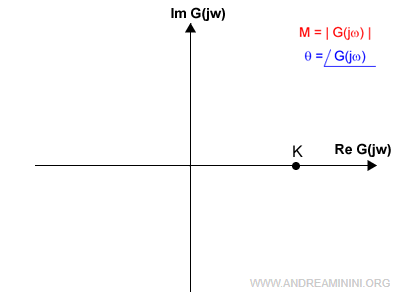
Se K<0 il punto si trova sempre sull'asse dei numeri reali ma a sinistra, con una fase φ(0)=±180° ossia un angolo di ±180°.
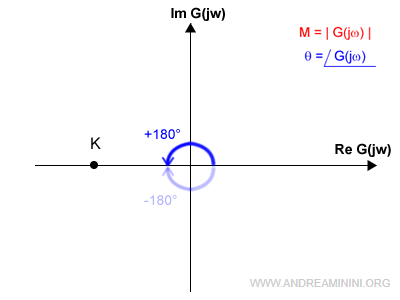
Una volta individuato il punto iniziale devo capire in che direzione si muove il diagramma.
A riguardo c'è una regola di tracciamento molto importamente: la funzione G(jw) abbandona l'asse reale sempre in modo ortogonale.
Quindi, possono verificarsi sei casi possibili.
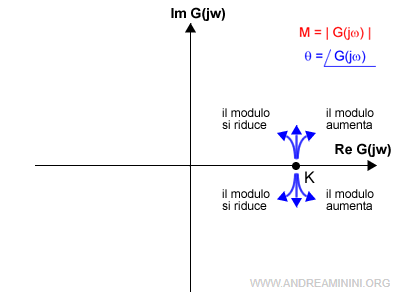
Le frecce che rientrano si verifcano quando il modulo si riduce al crescere delle pulsazioni ω.
Viceversa, le frecce che divergono all'esterno si presentano quando il modulo aumenta al crescere delle pulsazioni ω.
Caso 2 (h>0)
Se il valore h>0 nella funzione, allora il diagramma parte da un punto all'infinito.
$$ \lim_{ω \rightarrow 0^+} |G(jω)| = \infty $$
$$ \lim_{ω \rightarrow 0^+} arg[ G(jω) ] = -h \cdot \frac{π}{2} - φ_0 $$
Dove φ0=0 se K è positivo o φ0=π se K è negativo.
con una fase pari a
$$ φ(0)=arg(K) - h \cdot 90° =\begin{cases} h \cdot ( - 90°) \:\:\: se \: K>0 \\ \\ ±180° - h 90° \:\:\: se \: K<0 \end{cases} $$
Se non uso la funzione di trasferimento in forma fattorizzata φ0=0 se K1·b0/ah è positivo o φ0=π se K1·b0/ah è negativo.
Caso 3 (h<0)
Se il valore h<0 il diagramma di Nyquist parte dall'origine (0,0) del piano di Gauss.
$$ \lim_{ω \rightarrow 0^+} |G(jω)| = 0 $$
A questo punto posso studiare passare allo studio del comportamento asintotico della funzione.
2] Comportamento per ω → +∞
Analizzo il comportamento della funzione di trasferimento quando le pulsazioni ω tendono a più infinito.
$$ \lim_{ω \rightarrow +∞} G(jω) $$
A] Se la funzione di trasferimento G è una funzione razionale strettamente propria, ossia se il grado del polinomio al numeratore (m) è inferiore al grado del polinomio al denominatore (n), al crescere delle pulsazioni il modulo si riduce e il diagramma di Nyquist termina nell'origine (0,0) del piano complesso
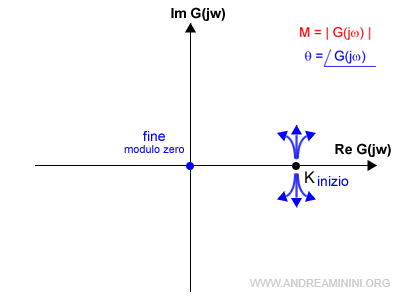
In questo caso $$ \lim_{ω \rightarrow +∞} G(jω) = 0 $$
B] Se la funzione di trasferimento G è una funzione razionale propria, ossia se il grado del polinomio al numeratore (m) è uguale al grado del polinomio al denominatore (n), il diagramma termina su un punto (K',0) dell'asse reale.
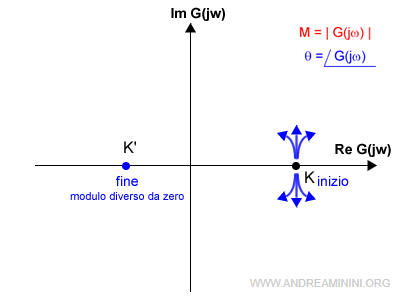
In questo caso $$ \lim_{ω \rightarrow +∞} G(jω) = K' $$
Un'altra regola di tracciamento importante del diagramma di Nyquist riguarda la fase di arrivo del diagramma.
La funzione giunge al punto finale del diagramma una fase pari a $$ φ(∞)=arg(K')-(n-m) \cdot (90°) =\begin{cases} -(n-m) 90° \:\:\: se \: K'>0 \\ \\ ±180° - (n-m) 90° \:\:\: se \: K'<0 \end{cases} $$.
Nota. Dove n e m sono parametri della funzione di trasferimento $$ G(s) = K_1 \cdot \frac{ s^m + b_{m-1}s^{m-1}+...+_1s+b_0 }{ s^h (s^{n-h}+a_{n-1}s^{n-h-1}+...+a_{h+1}s+a_h } $$
Un esempio pratico
Ho la seguente funzione di trasferimento con K>0 e τ>0
$$ F(s) = \frac{K}{1+τs} $$
La funzione ha un solo polo e nessuno zero.
$$ p_1 = \frac{-1}{τ} $$
Lo stato della funzione è h=0.
Inizio del diagramma (ω=0)
Poiché lo stato h=0, quando le pulsazioni sono ω=0 il diagramma di Nyquist parte dalle coordinate (K,0) del piano complesso.
Per l'ipotesi iniziale K>0. Quindi si tratta di un punto del semiasse reale positivo.
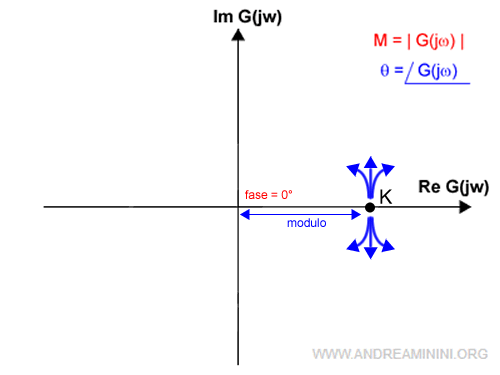
Essendo K>0 la fase è pari a zero gradi
$$ φ(0)=0° $$
Dal punto (K,0) ci sono diverse direzioni che il diagramma può prendere.
Fine del diagramma (ω→ ∞)
La funzione è strettamente propria perché il grado del polinomio al numeratore (m) è inferiore al grado del polinomio al denominatore (n).
$$ n - m = 1 $$
Quindi, il diagramma di Nyquist termina all'origine (0,0) del piano complesso.
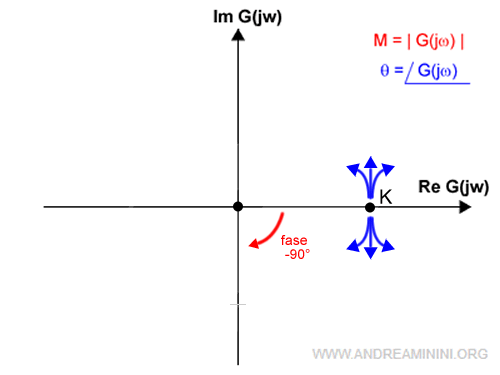
La componente K' è sicuramente positiva perché K e τ sono positivi per l'ipotesi iniziale
$$ K' = \frac{K}{τ} $$
Quindi, la fase per ω→∞ è di -90°
$$ φ(+∞) = -90° $$
Ricapitolando, la fase φ della funzione di trasferimento F(s) è compresa tra 0° e -90°.
Pertanto, il diagramma di Nyquist si trova sempre nel quarto quadrante del piano complesso (il quadrante in basso a destra).
Elimino così tre possibili direzioni a partire dal punto iniziale (K,0).
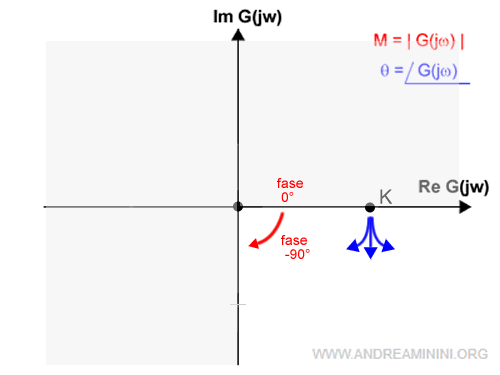
In questo caso il modulo si riduce con le pulsazioni ω→∞ e il diagramma converge all'origine del piano di Gauss.
Quindi, posso eliminare anche due delle tre frecce restanti.
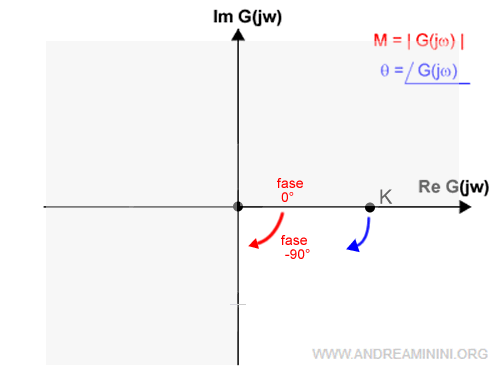
In questo modo ho individuato la direzione e il verso del diagramma a partire da K.
Dalle informazioni ottenute so che il modulo tende ad annullarsi con le pulsazioni ω→∞ e il diagramma converge all'origine con un angolo finale di -90°.
Quindi, il diagramma di Nyquist è approssimativamente il seguente
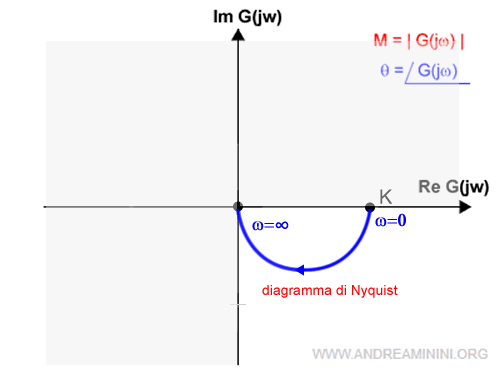
Ho individuato il diagramma di Nyquist per l'intervallo positivo (0,+∞) delle pulsazioni ω.
E per valori negativi delle pulsazioni?
Sapendo che il diagramma nell'intervallo negativo (-∞,0) è simmetrico al precedente rispetto all'asse reale.
Posso facilmente ricostruire il diagramma anche nell'intervallo negativo.
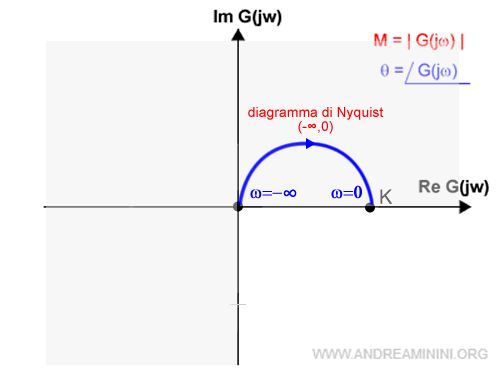
Nota. Se K fosse negativo (K<0) il diagramma si troverebbe nel secondo quadrante con τ>0
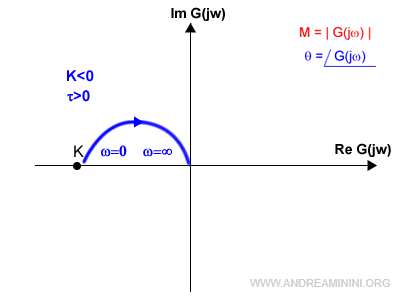
oppure nel terzo quadrante con τ<0
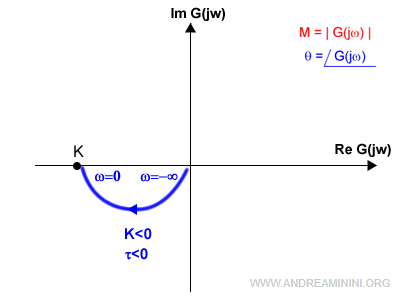
E così via.
