La radice ennesima dell'unità

La radice n-esima dell'unità è un numero complesso z tale che la potenza ennesima di z è uguale a $$ z^n = 1 $$ Pertanto $$ \sqrt[n]{z^n} = \sqrt[n]{1} $$ $$ z = \sqrt[n]{1} $$

In forma trigonometrica la radice ennesima dell’unità è

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$

Dove k=0, 1, 2, ..., n-1

Un esempio pratico

La radice quadrata dell'unità ha n=2 soluzioni

Per k=0 la prima soluzione è

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$

$$ \sqrt[2]{1} = \cos \frac{ 2 \cdot 0 \cdot \pi }{2} + i \cdot \sin \frac{ 2 \cdot 0 \cdot \pi }{2} $$

$$ \sqrt[2]{1} = \cos 0 + i \cdot \sin 0 $$

$$ \sqrt[2]{1} = 1 + i \cdot 0 $$

$$ \sqrt[2]{1} = 1 $$

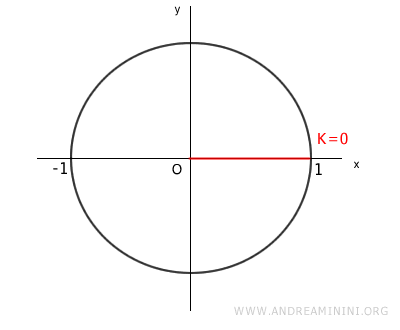
Per k=1 la seconda soluzione è

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$

$$ \sqrt[2]{1} = \cos \frac{ 2 \cdot 1 \cdot \pi }{2} + i \cdot \sin \frac{ 2 \cdot 1 \cdot \pi }{2} $$

$$ \sqrt[2]{1} = \cos \frac{ 2\pi }{2} + i \cdot \sin \frac{ 2 \cdot \pi }{2} $$

$$ \sqrt[2]{1} = \cos \pi + i \cdot \sin \pi $$

$$ \sqrt[2]{1} = -1 + i \cdot 0 $$

$$ \sqrt[2]{1} = - 1 $$

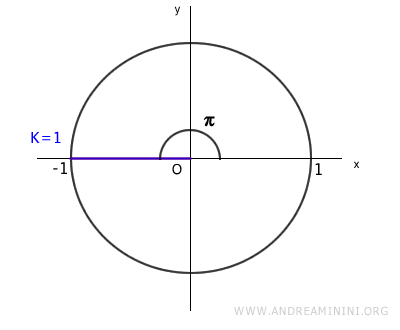
Nota. Per ogni valore k>1 le radici si ripetono ciclicamente alternandosi tra 1 e -1. Ad esempio, per k=2 la radice è 1. Per k=3 la radice è -1. E via dicendo. Per questa ragione nella radice quadrata dell'unità si considerano solo le prime due soluzioni distinte: 1 e -1. Più in generale, per una radice n-esima dell'unità si considerano le prime n soluzioni.

La dimostrazione

Parto dal presupposto che

$$ z^n = 1 $$

Riscrivo il numero complesso in forma trigonometrica

$$ [d \cdot ( \cos \alpha + i \sin \alpha) ]^n = 1 $$

Sapendo che 1 in forma triconometrica è cos(0)+i·sin(0)

$$ [d \cdot ( \cos \alpha + i \sin \alpha) ]^n = \cos 0 + i \cdot \sin 0 $$

Il modulo al secondo membro è uguale a 1

$$ [d \cdot ( \cos \alpha + i \sin \alpha) ]^n = 1 \cdot ( \cos 0 + i \cdot \sin 0 ) $$

Applico al primo membro la formula di De Moivre sulla potenza dei numeri complessi

$$ d^n \cdot ( \cos n\alpha + i \sin n\alpha) ) = 1 \cdot ( \cos 0 + i \cdot \sin 0 ) $$

L'uguaglianza è valida anche per i multipli di 2kπ

$$ d^n \cdot ( \cos n\alpha + i \sin n\alpha) ) = 1 \cdot [ \cos ( 0 + 2k \pi) + i \cdot \sin ( 0 + 2k \pi) ] $$

Per confronto tra i due membri deduco che

$$ \begin{cases} d^n = 1 \\ \\ n \alpha = 0 + 2k \pi \end{cases} $$

Pertanto l'angolo alfa è

$$ \begin{cases} d^n = 1 \\ \\ \alpha = \frac{ 2k \pi }{n} \end{cases} $$

Quindi, la radice n-esima dell'unità è

$$ \sqrt[n]{1} = \cos \frac{ 2k \pi }{n} + i \cdot \sin \frac{ 2k \pi }{n} $$

per ogni k intero.

E così via.