La derivata dell'arcotangente

La derivata dell'arcotangente è $$ D[\arctan x] = \frac{1}{1+x^2} $$

Per ottenere la formula basta ricordarsi che l'arcotangente è la funzione inversa della tangente.

Quindi, basta usare la regola di derivazione delle funzioni inverse.

Dimostrazione e spiegazione

La tangente è una funzione trigonometrica continua ma non monotona su R.

$$ f(x) = \tan x $$

Tuttavia, se la analizzo nell'intervallo aperto (-π/2,π/2) la tangente è monotona e strettamente crescente.

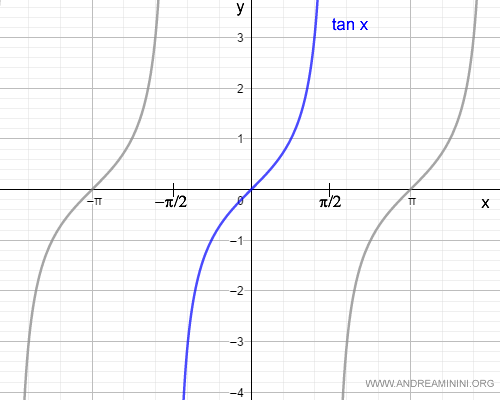
Pertanto, nell'intervallo aperto (-π/2,π2) la funzione tan x è invertibile e la sua funzione inversa è l'arcotangente:

$$ f^{-1}( y = \tan x ) = \arctan x $$

Cos'è l'arcotangente? Dal punto di vista geometrico l'arcotangente misura l'arco sulla circonferenza ossia l'angolo α in radianti (o gradi) che determina il valore del coseno.

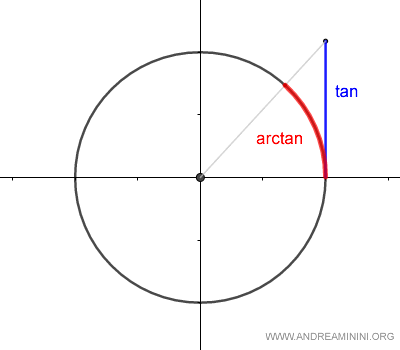
Pertanto, tangente e arcotangente sono funzioni inverse l'una dell'altra
$$ y = \tan α $$ $$ α = \arctan y $$ Di conseguenza $$ y = \tan ( \arctan y ) $$ $$ α = \arctan ( \tan α ) $$

La funzione arcotangente ha il campo di definizione ( dominio ) in tutto l'insieme dei numeri reali R e il codominio nell'intervallo (-π/2,π/2).

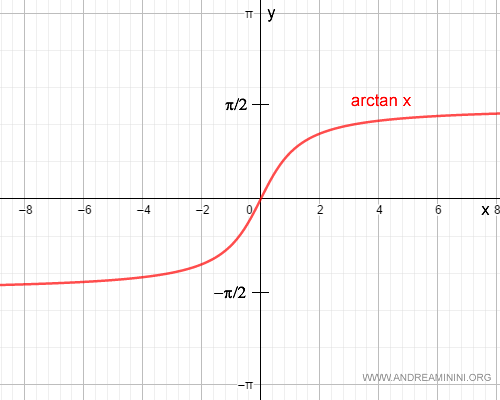
Il limite dell'arcotangente per più infinito è π/2 e per meno infinito è -π/2.

$$ \lim_{x \rightarrow +∞} \arctan x = \frac{π}{2} $$

$$ \lim_{x \rightarrow -∞} \arctan x = - \frac{π}{2} $$

Pertanto, la funzione arcotangente è derivabile in R.

Per calcolare la derivata dell'arcotangente uso la regola di derivazione di una funzione inversa.

$$ D[f(x)] = \frac{1}{D[f^{-1}(x)]} $$

$$ D[ \arctan x] = \frac{1}{D[ \tan y ]} $$

La derivata della tangente è 1/cos² y

$$ D[ \arctan x] = \frac{1}{ \frac{1}{\cos^2 y} } $$

Nota. Sapendo che cos² y + sin² y = 1 posso sostituire uno al denominatore con cos² y + sin² y

$$ D[ \arctan x] = \frac{1}{ \frac{ \cos^2 y + \sin^2 y }{\cos^2 y} } $$

$$ D[ \arctan x] = \frac{1}{ \frac{ \cos^2 y }{\cos^2 y} + \frac{ \sin^2 y }{\cos^2 y} } $$

$$ D[ \arctan x] = \frac{1}{ 1 + \frac{ \sin^2 y}{\cos^2 y} } $$

Nota. Sapendo che tan y = sin y \ cos y allora l'elevazione a potenza è tan² y = sin² y/cos²y

$$ D[ \arctan x] = \frac{1}{ 1 + \tan^2 y } $$

Nota. Sapendo che y=arctan x

$$ D[ \arctan x] = \frac{1}{ 1 + \tan^2 ( \arctan x ) } $$

Nota. Poiché la tangente e l'arcotangente sono inverse l'una dell'altra. $$ y = \arctan x \\ x = \tan y $$ allora $$ \tan ( \arctan x ) = x $$ Quindi $$ \tan^2 ( \arctan x ) = x^2 $$

$$ D[ \arctan x] = \frac{1}{ 1 + x^2 } $$

Ho così dimostrato la formula della derivata dell'arcotangente.

E così via.