La derivata di una potenza
Definizione
La regola per derivare una potenza è la seguente: $$ D[ax^b]=b \cdot a x^{b-1} $$
Per spiegare questa semplice regola di derivazione, svolgo la dimostrazione e un esempio pratico.
La dimostrazione
Dimostrazione per induzione
La derivata di xn per n=1 è uguale a 1.
$$ D[x^1] = 1 \cdot x^0 = 1 $$
Suppongo che la regola di derivazione si valida per n=k qualsiasi.
$$ D[x^k] = k \cdot x^{k-1} $$
Poi verifico se la regola è valida anche per n=k+1 ossia per l'intero successivo.
$$ D[x^{k+1}] $$
Posso riscrivere la precedente funzione come prodotto di due variabili.
$$ D[x \cdot x^k] $$
A questo punto applico la regola di derivazione del prodotto di due funzioni.
$$ D[x \cdot x^k] = 1 \cdot x^k + x \cdot k \cdot x^{k-1} $$
$$ D[x \cdot x^k] = 1 \cdot x^k + k \cdot x^k $$
$$ D[x \cdot x^k] = (1+k) \cdot x^k $$
Questo dimostra la regola di dervizione.
Esempio
Data la seguente funzione
$$ f(x) = x^2 $$
Secondo la regolare di derivazione, la derivata prima della funzione f(x) dovrebbe essere
$$ f'(x) = (2) \cdot x^{2-1} = 2x $$
Per verificarlo calcolo il limite del rapporto incrementale della funzione per h tendente a zero.
$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
So già che
$$ f(x) = x^2 $$
$$ f(x+h) = (x+h)^2 $$
Quindi sostituisco le funzioni nel rapporto incrementale.
$$ f'(x) = \lim_{h \rightarrow 0} \frac{(x+h)^2-x^2}{h} $$
Poi semplifico il rapporto svolgendo i calcoli algebrici
$$ f'(x) = \lim_{h \rightarrow 0} \frac{x^2+2xh+h^2-x^2}{h} $$
$$ f'(x) = \lim_{h \rightarrow 0} \frac{2xh+h^2}{h} $$
$$ f'(x) = \lim_{h \rightarrow 0} \frac{h(2x+h)}{h} $$
$$ f'(x) = \lim_{h \rightarrow 0} 2x+h $$
Il limite fa tendere h a zero. Pertanto, il risultato del limite è
$$ f'(x) = 2x $$
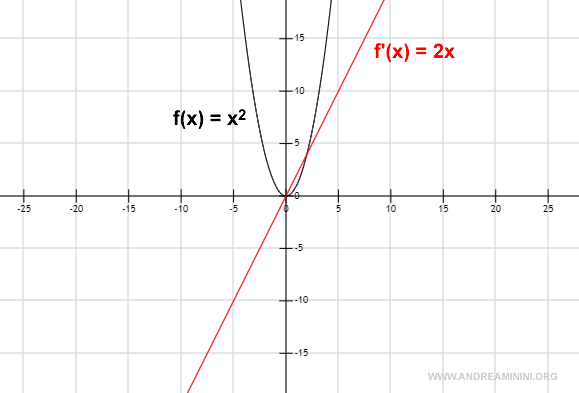
Ho così dimostrato che la derivata di x2 è 2x.
La rappresentazione grafica
A questo punto verifico se la regola di derivazione vale anche per k+1
$$ D[x^{2+1}] $$
Trasformo la funzione x2+1 in un prodotto x·x2
$$ D[x \cdot x^2] $$
Poi applico la regola di derivazione del prodotto di due funzioni
$$ D[x] \cdot x^2 + x \cdot D[x^2] $$
$$ 1 \cdot x^2 + x \cdot 2x $$
$$ x^2 + 2x^2 $$
$$ 3x^2 $$
La derivata prima di x3 è 3x2.
Ho così dimostrato che la regola vale anche k+1
Quindi, per induzione la regola è valida per qualsiasi intero positivo.
Un esempio pratico
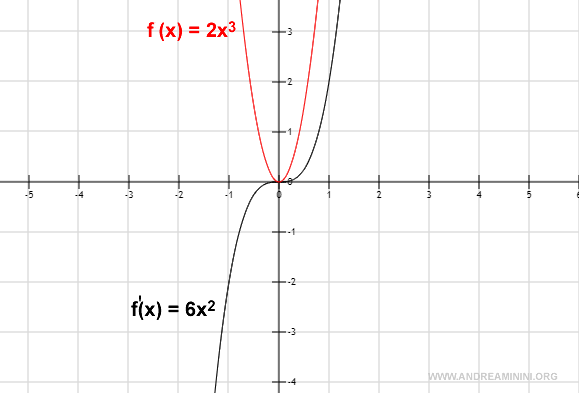
In quest'altro esempio calcolo la derivata prima di 2x3.
$$ f(x) = 2x^3 $$
Secondo la regola di derivazione
$$ f'(x) = 3 \cdot 2x^{3-1}= 6x^2 $$
Verifica
Calcolo il limite del rapporto incrementale della funzione per h tendente a zero
$$ f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
dove
$$ f(x)=2x^3 $$
$$ f(x+h)=2(x+h)^3 $$
Sostituisco le funzioni nel rapporto incrementale
$$ f'(x) = \lim_{h \rightarrow 0} \frac{2(x+h)^3-2x^3}{h} $$
Poi svolgo i calcoli algebrici
$$ f'(x) = \lim_{h \rightarrow 0} \frac{2(x^3+
3x^2h + 3xh^2 + h^3) -2x^3}{h} $$
$$ f'(x) = \lim_{h \rightarrow 0} \frac{2x^3+
6x^2h + 6xh^2 + 2h^3 -2x^3}{h} $$
$$ f'(x) = \lim_{h \rightarrow 0} \frac{
6x^2h + 6xh^2 + 2h^3 }{h} $$
$$ f'(x) = \lim_{h \rightarrow 0} \frac{
h(6x^2 + 6xh + 2h^2 ) }{h} $$
$$ f'(x) = \lim_{h \rightarrow 0}
6x^2 + 6xh + 2h^2 $$
Il limite fa tendere la variabile h a zero e annulla 6xh e 2x2.
Pertanto, il limite del rapporto incrementale è
$$ f'(x) = 6x^2 $$
La derivata prima di 2x3 è 6x2.
La rappresentazione grafica