La matrice inversa con il metodo di Gauss
Il metodo di Gauss è un metodo alternativo per calcolare la matrice inversa.
E' particolarmente utile quando la matrice invertibile è di grandi dimensioni.
Come calcolare la matrice inversa con il metodo di Gauss
Per prima cosa affianco una matrice identità I a destra della matrice M
In questo modo formo una matrice rettangolare M|I
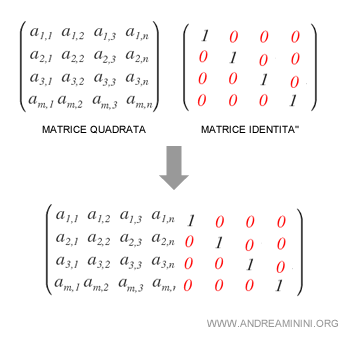
Nella matrice M|I la matrice identità si trova nella sezione di destra (rossa).
A questo punto uso le mosse di Gauss per ottenere una matrice identità nella sezione di sinistra.
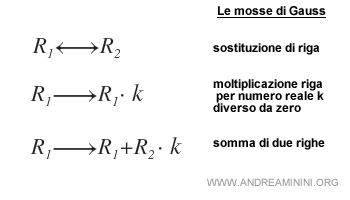
Nota. Le mosse di Gauss sono lo scambio tra due righe, la moltiplicazione di una riga per un numero reale k diverso da zero e la somma di una riga con un'altra riga moltiplicata per k.
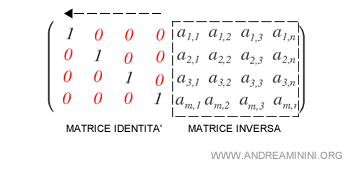
Se riesco a ottenere una matrice identità nella sezione di sinistra, allora la matrice quadrata nella sezione a destra è la matrice inversa di M.
Un esempio pratico
Considero una semplice matrice quadrata 2x2
$$ M = \begin{pmatrix} 2 & 1 \\ -1 & 1 \end{pmatrix} $$
Uso il metodo di Gauss per calcolare la sua matrice inversa M-1
Aggiungo una matrice identità 2x2 (I) a destra della matrice M
$$ M|I = \begin{pmatrix} 2 & 1 & 1 & 0 \\ -1 & 1 & 0 & 1 \end{pmatrix} $$
A questo punto cerco di trasformare la matrice 2x2 a sinistra in una matrice identità usando le mosse di Gauss.
Scambio le posizioni tra le righe R1⇔R2
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 & 1 & 1 & 0 \end{pmatrix} $$
Sommo alla seconda riga la prima riga moltiplicata per due ossia R2=R2+R1·2
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ 2 + (-1) \cdot 2 & 1 + 1 \cdot 2 & 1 + 0 \cdot 2 & 0 + 1 \cdot 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} -1 & 1 & 0 & 1 \\ \color{red}0 & 3 & 1 & 2 \end{pmatrix} $$
Ora sottraggo alla prima riga la seconda riga moltiplicata per 1/3 ossia R1=R1+R1·1/3
$$ M|I = \begin{pmatrix} -1 - 0 \cdot \frac{1}{3} & 1 - 3 \cdot \frac{1}{3} & 0 - 1 \cdot \frac{1}{3} & 1 - 2 \cdot \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} -1 & \color{red}0 & - \frac{1}{3} & \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
Moltiplico la prima riga per meno -1 ossia R1=R1·(-1)
$$ M|I = \begin{pmatrix} -1 \cdot (-1) & 0 \cdot (-1) & - \frac{1}{3} \cdot (-1) & \frac{1}{3} \cdot (-1) \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
$$ M|I = \begin{pmatrix} \color{red}1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & 3 & 1 & 2 \end{pmatrix} $$
Moltiplico la seconda riga per -1/3 ossia R2=R2·(1/3)
$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 \cdot \frac{1}{3} & 3 \cdot \frac{1}{3} & 1 \cdot \frac{1}{3} & 2 \cdot \frac{1}{3} \end{pmatrix} $$
$$ M|I = \begin{pmatrix} 1 & 0 & \frac{1}{3} & - \frac{1}{3} \\ 0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
Ho ottenuto una matrice identità nella sezione di sinistra.
$$ M|I = \begin{pmatrix} \color{red} 1 & \color{red}0 & \frac{1}{3} & - \frac{1}{3} \\ \color{red}0 & \color{red}1 & \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
Pertanto, la matrice M è una matrice invertibile.
La sua matrice inversa è la matrice nella sezione di destra
$$ M|I = \begin{pmatrix} 1 & 0 & \color{red}{ \frac{1}{3} } & \color{red} { - \frac{1}{3} } \\ 0 & 1 & \color{red}{ \frac{1}{3} } & \color{red} { \frac{2}{3} } \end{pmatrix} $$
Quindi la matrice inversa di M è la seguente:
$$ M^{-1} = \begin{pmatrix} \frac{1}{3} & - \frac{1}{3} \\ \frac{1}{3} & \frac{2}{3} \end{pmatrix} $$
Nota. Questo esercizio "giocattolo" l'ho svolto con gli altri metodi di calcolo della matrice inversa giungendo allo stesso risultato.
