Termodinamica dell'equilibrio chimico
Dal punto di vista della termodinamica, un processo è in equilibrio chimico se la variazione di energia libera di Gibbs è nulla.
$$ \Delta G = H - TS = 0 $$
Dove H è l'entalpia, T è la temperatura e S è l'entropia.
A parità di temperatura, la condizione ΔG=0 si verifica a un particolare stato di avanzamento della reazione chimica, quando la quantità relativa delle sostanze diventa costante.
Inizialmente l'energia libera G del sistema diminuisce al variare della composizione, seguendo un andamento a U.
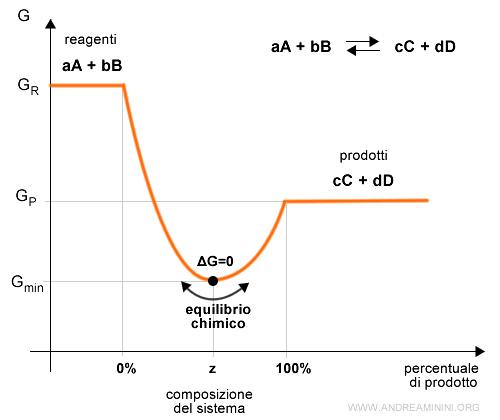
Nel punto di minimo il sistema raggiunge spontaneamente una variazione di energia libera nulla ossia ΔG=0.
Il minimo di energia libera si stabilizza una particolare composizione (z) dei reagenti e dei prodotti.
In questo punto di raggiunge un equilibrio chimico dinamico.
La dimostrazione
Prendo in considerazione una generica reazione chimica non necessariamente in equilibrio
$$ aA+bB \leftrightharpoons cC+dD $$
Dove a,b,c,d sono i coefficienti stechiometrici mentre A,B,C,D sono le specie chimiche coinvolte nella reazione.
La variazione di energia libera ΔG dipende dalla differenza di energia libera tra i prodotti e i reagenti.
$$ \Delta G = \sum G_{prodotti} - \sum G_{reagenti} $$
Sapendo che in termodinamica l'energia libera G è pari a
$$ G = H-TS $$
Dove H è l'entalpia, T è la temperatura e S è l'entropia.
Poiché l'entalpia è H = E + PV posso sostituire
$$ G = (E+PV)-TS $$
Dove E è l'energia interna, P è la pressione e V è il volume.
Per il 1° principio della termodinamica l'energia interna è E=Q-L.
$$ G = ((Q-L)+PV)-TS $$
Dove Q è il calore e L è il lavoro.
Dopo queste modifiche la formula equivalente dell'energia libera è diventata la seguente:
$$ G = Q-L+PV-TS $$
Calcolo la derivata di G per ottenere la variazione di energia libera
$$ dG = d[Q-L+PV-TS] $$
$$ dG = dQ -dL+d[PV]-d[TS] $$
$$ dG = dQ -dL+VdP + PdV - SdT - TdS $$
In questo caso il calore è reversibile dQ=dQrev perché la reazione chimica è reversibile,
$$ dG = dQ_{rev} -dL+VdP + PdV - SdT - TdS $$
Sapendo che in un processo reversibile la variazione del lavoro è dL = PdV
$$ dG = dQ_{rev} - PdV +VdP + PdV - SdT - TdS $$
$$ dG = dQ_{rev} +VdP - SdT - TdS $$
Sapendo che la variazione di entropia in un processo reversibile è dS=dQrev/T
Quindi TdS = dQrev
$$ dG = dQ_{rev} +VdP - SdT - dQ_{rev} $$
$$ dG = VdP - SdT $$
Poiché il processo avviene a temperatura costante, la derivata di una costante è nulla. Quindi dT=0
$$ dG = VdP - S \cdot 0 $$
$$ dG = VdP $$
Sapendo che l'equazione generale dei gas è nPV=RT
Considerando una sola mole (n=1) diventa PV=RT
Quindi V=RT/P
$$ dG = VdP $$
$$ dG = (\frac{RT}{P}) dP $$
Per calcolare l'energia libera G integro entrambi i membri rispettivamente da G a G° e da P a P°.
$$ \int_{G°}^G dG = \int_{P°}^P (\frac{RT}{P}) dP $$
Dove G° e P° sono l'energia libera standard e la pressione standard.
Mentre G e P sono un qualsiasi valore dell'energia libera e della pressione della reazione chimica.
Nota. I valori standard dell'energia libera e della pressione sono rilevati a 1 atm di pressione e 25°C di temperatura.
Il prodotto RT è costante, quindi può uscire dall'integrale.
$$ \int_{G°}^G dG = RT \cdot \int_{P°}^P (\frac{1}{P}) dP $$
Svolgo i due integrali
$$ [G]_{G°}^G = RT \cdot [\log P ]_{P°}^P $$
$$ G-G° = RT \cdot ( \log P - \log P°) $$
Applico la regola della differenza tra due logaritmi naturali
$$ G-G° = RT \cdot \log \frac{P}{P°} $$
e ottengo l'energia libera
$$ G =G° + RT \cdot \log \frac{P}{P°} $$
Nel caso di una generica reazione di questo tipo
$$ aA+bB \leftrightharpoons cC+dD $$
la variazione dell'energia libera è la differenza tra l'energia libera dei prodotti meno quella dei reagenti.
$$ \Delta G = G_{prodotti} - G_{reagenti} $$
$$ \Delta G = [cG°_C + RT \log (\frac{P_C}{P°})^c ] + [dG°_D + RT \log (\frac{P_D}{P°})^d ] + \\ \:\:\:\:\:\:\:\: - [aG°_A + RT \log (\frac{P_A}{P°})^a ] - [bG°_B + RT \log (\frac{P_B}{P°})^b ] $$
$$ \Delta G = (cG°_C + dG°_D) - (aG°_A+bG°_B) + ( RT \log (\frac{P_C}{P°})^c + RT \log (\frac{P_D}{P°})^d ) + \\ \:\:\:\:\:\:\:\: - ( RT \log (\frac{P_A}{P°})^a ) + ( RT \log \frac{P_B}{P°})^b ) $$
$$ \Delta G = (cG°_C + dG°_D) - (aG°_A+bG°_B) + \\ \:\:\:\:\:\:\:\: + RT \cdot [ ( \log (\frac{P_C}{P°})^c + \log ( \frac{P_D}{P°})^d ) - ( \log (\frac{P_A}{P°})^a + \log ( \frac{P_B}{P°})^b ) ] $$
$$ \Delta G = (cG°_C + dG°_D) - (aG°_A+bG°_B) + \\ \:\:\:\:\:\:\:\: + RT \cdot [ \log ( (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d ) - \log ( (\frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b ) ] $$
$$ \Delta G = (cG°_C + dG°_D) - (aG°_A+bG°_B) + RT \cdot \log \frac{ (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d }{ ( \frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b } $$
In condizioni di equilibrio chimico ΔG=0
$$ 0 = (cG°_C + dG°_D) - (aG°_A+bG°_B) + RT \cdot \log \frac{ (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d }{ ( \frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b } $$
In questo modo posso calcolare la variazione dell'energia libera standard ΔG°
$$ (cG°_C + dG°_D) - (aG°_A+bG°_B) = - RT \cdot \log \frac{ (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d }{ ( \frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b } $$
ossia
$$ \Delta G° = - RT \cdot \log \frac{ (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d }{ ( \frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b } $$
Essendo la temperatura costante anche la variazione dell'energia standard ΔG° è una costante.
Sapendo che al secondo membro RT è costante, questo vuol che anche il logaritmo è costante e posso sostituirlo con una costante Kp*.
$$ \Delta G° = - RT \cdot \log \cdot K_p* $$
Dove Kp* è la costante termodinamica dell'equilibrio a pressioni parziali.
$$ K_p* = \frac{ (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d }{ ( \frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b } $$
che si può scrivere anche in questa forma equivalente
$$ K_p* = \frac{ P_C^c \cdot P_D^d}{P_A^a \cdot P_B^b} \cdot ( \frac{1}{P°} )^{(c+d-a-b)} $$
Nota. I vari passaggi algebrici per passare a quest'ultima forma. $$ K_p* = \frac{ (\frac{P_C}{P°})^c \cdot ( \frac{P_D}{P°})^d }{ ( \frac{P_A}{P°})^a \cdot ( \frac{P_B}{P°})^b } $$ $$ K_p* = \frac{ \frac{P_C^c}{P°^c} \cdot \frac{P_D^d}{P°^d} }{ \frac{P_A^a}{P°^a} \cdot \frac{P_B^b}{P°^b} } $$ $$ K_p* = \frac{P_C^c}{P°^c} \cdot \frac{P_D^d}{P°^d} \cdot ( \frac{P°^a}{P_A^a} \cdot \frac{P°^b}{P_B^b} ) $$ $$ K_p* = \frac{P_C^c \cdot P_D^d}{P_A^a \cdot P_B^b } \cdot \frac{P°^a \cdot P°^b}{P°^c \cdot P°^d} $$ $$ K_p* = \frac{P_C^c \cdot P_D^d}{P_A^a \cdot P_B^b } \cdot P°^{a+b-c-d} $$ $$ K_p* = \frac{P_C^c \cdot P_D^d}{P_A^a \cdot P_B^b } \cdot \frac{1}{P°^{c+d-a-b}} $$
Per semplicità indico la somma algebrica Δn=c+d-a-b
$$ K_p* = \frac{ P_C^c \cdot P_D^d}{P_A^a \cdot P_B^b} \cdot ( \frac{1}{P°} )^{\Delta n} $$
Il primo termine al secondo membro è la costante di equilibrio a pressioni parziali Kp.
$$ K_p* = K_p \cdot ( \frac{1}{P°} )^{\Delta n} $$
In condizioni di equilibrio
Allo stesso modo posso indicare la variazione di energia libera con la costante di equilibrio a concentrazione.
$$ \Delta G° = - RT \cdot \log \cdot K_c* $$
Dove Kc* considera le concentrazioni delle specie chimiche nei reagenti e nei prodotti.
$$ K_c* = \frac{ [C]^c \cdot [D]^d}{[A]^a \cdot [B]^b} \cdot ( \frac{1}{C°} )^{\Delta n} $$
Quindi, in modo analogo posso anche trovare una relazione tra la costante di equilibrio a concentrazione Kc* e Kc.
$$ K_c* = K_c \cdot ( \frac{1}{C°} )^{\Delta n} $$
A cosa serve la relazione tra la variazione di energia libera standard e la costante di equilibrio?
La relazione tra ΔG° e K* permette di fare previsioni sul verso della reazione:
- Se K°>1 e ΔG°<0 la reazione aumenta i prodotti
- Se K°<1 e ΔG°>0 la reazione aumenta i reagenti
Dove K° è sempre un valore maggiore di zero.
Non può essere uguale a zero perché implicherebbe l'assenza della reazione.
E così via.
