La sintesi supervisiva
La sintesi supervisiva è un procedimento per determinare qual è la struttura del supervisore S/P di un processo P quando devo imporre una particolare specifica dinamica K. $$ L(S/P)=L(P)||K $$
La premessa
Il sistema SED a ciclo aperto P ha un linguaggio L(P) generato da un alfabeto E.
$$ L(P)⊆E* $$
Dove E* è l'insieme delle combinazioni possibili dei simboli dell'alfabeto E.
A partire da una specifica K devo costruire il supervisore S ossia un sistema a ciclo chiuso S/P.
Il supervisore è ammissibile se il linguaggio L(S/P) è la composizione concorrente del linguaggio del processo a ciclo aperto L(P) e del linguaggio della specifica K
$$ L(S/P) = L(P) \: || \: K $$
Nota. Il sistema a ciclo chiuso genera le parole w accettate simultaneamente da P e da K. Pertanto, si tratta di un sottoinsieme delle parole accettate dal sistema a ciclo aperto.
L'insieme degli eventi E (alfabeto) del sistema S/P è partizionato in eventi controllabili dal supervisore Ec ed eventi non controllabili dal supervisore Enc.
$$ E = E_c ∪ E_{nc} $$
Questo problema è stato studiato da Ramadge e Wonham negli anni '80, introducendo il concetto di linguaggio controllabile
Nota. Se ci sono più specifiche dinamiche K' e K'' a determinare l'automa a ciclo chiuso S/P, è sempre possibile determinare un'unica specifica K=K1||K2 pari alla composizione concorrente delle precedente.
Teorema di Ramadge e Wonham
Il supervisore S/P di un processo P esiste se e solo se il linguaggio della specifica dinamica totale K del supervisore è un linguaggio controllabile rispetto a P e Enc.
Se la specifica dinamica totale è controllabile rispetto a P e Enc, allora anche le specifiche dinamiche parziali dell'alfabeto E' di E sono controllabili.
Il linguaggio controllabile
Un linguaggio K è detto linguaggio controllabile rispetto al processo P e all'insieme dei simboli non controllabili Enc se l'intersezione tra L(P) e la concatenazione KEnc è un sottoinsieme del linguaggio K. $$ L(P) ⋂ KE_{nc} ⊆ K $$
Dove la sigla KEnc è la concatenazione delle parole del linguaggio supervisore K e gli eventi non controllabili del processo P.
Ogni elemento dell'insieme KEnc è una parola w composta da un prefisso w' (parola di K) e un simbolo s di Enc. $$ w=w's $$
Il prefisso w' è sicuramente una sequenza di eventi accettata da K.
La concatenazione w's non è però detto che appartenga a K.
- Se l'evento s è controllabile (s∈Ec) la parola w's appartiene a K perché il supervisore può disabilitare o abilitare l'evento s. Ma in questo caso s è un evento non controllabile per definizione (s∈Enc). Quindi, questa ipotesi va scartata nel caso del linguaggio controllato.
- Se l'evento s è non controllabile (s∈Enc) allora la parola w's può appartenere o meno a L(S/P). La parola w's∈L(S/P) se w's↑E∈L(P) e w's↑E'∈K. Se una o entrambe le proiezioni non sono soddisfatte w's∉L(S/P).
Il supervisore abilitante
In un sistema supervisionato S/P il supervisore S è detto supervisore abilitante (o Enc abilitante) rispetto a P, se il supervisore non disabilita nessun evento non controllabile.
A cosa serve sapere se il supervisore è abilitante
Se l'automa S è abilitante rispetto a P, la specifica K=L(s), ossia il linguaggio dell'automa, è un linguaggio controllabile rispetto a P.
In questo caso il modello supervisionato S/P non genera nessuno stato incontrollabile.
Nota. In pratica, il supervisore non deve disabilitare gli eventi non controllabili di S/P. Se ne disabilita anche uno solo, il supervisore non va bene. Ovviamente, questo può accadere soltanto se l'insieme degli eventi E' del supervisore contiene eventi non controllabili. Se contiene tutti eventi controllabili, il problema non si pone e la specifica è sicuramente controllabile.
Viceversa, se l'automa non è abilitante rispetto a P, la specifica è non controllabile e potrebbero verificarsi degli stati incontrollabili.
Come capire se un supervisore S è abilitante rispetto a P
Per farlo c'è una semplice regola da applicare
Il supervisore non è abilitante se esiste almeno un evento non controllabile s di Ec attivo in uno stato xi del sistema aperto s in A(xi) ma non attivo nello stato xi,j nel sistema supervisionato S/P s $$ \exists s \in E_{nc} : s \in A(x_i) ∧ s \notin A(x_{i,j}) $$
Un esempio pratico
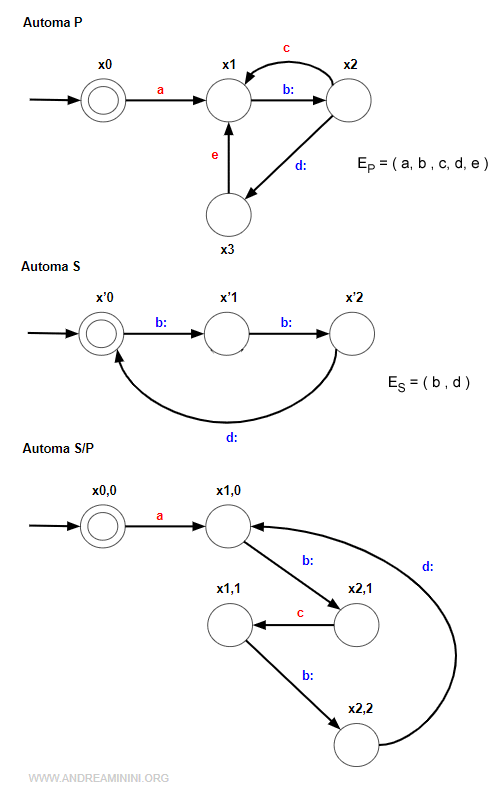
Ho un sistema a ciclo aperto P con quattro stati {x0,x1,x2,x3} e cinque eventi {a,b,c,d,e}.
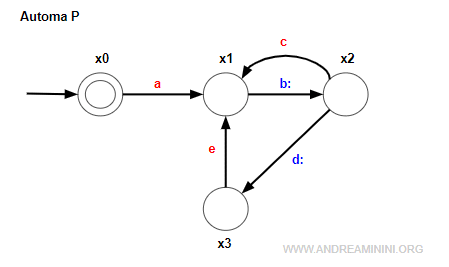
Il sistema ha due eventi controllabili Ec={b,d} e tre eventi non controllabili Enc={a,c,e}
L'insieme degli eventi del sistema P è
$$ E= \{ a,b,c,d,e \} $$
Voglio applicare una specifica K che imponga l'evento "d" ogni due eventi "b".
Per realizzare la specifica K affianco a P un l'automa S supervisore composto da quattro stati (x'0, x'1, x'2, x'3) e tre eventi {b,d,c}.
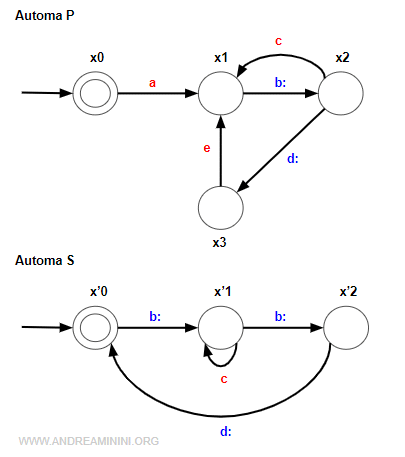
L'insieme degli eventi del supervisore è E'⊆E
$$ E' = \{ b,d,c \} $$
Gli eventi "b" e "d" sono eventi controllabili. Quindi, posso ignorarli.
L'evento "c" è, invece, un evento non controllabile.
Pertanto, devo verificare che il supervisore non disabiliti l'evento "c".
Per capire se il supervisore S è abilitante rispetto a P, elaboro la composizione concorrente degli automi S e P.
$$ L(S/P) = S ↑ P $$
In questo modo ottengo l'automa S/P (supervisionato)
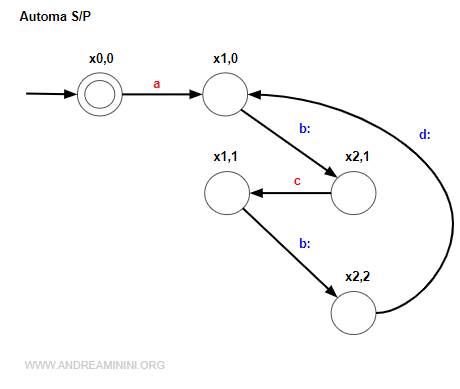
Nota. L'automa S/P è determinato dalla composizione concorrente S ↑ P. In ogni stato xi,j della rete S/P ho aggiunto in pedice lo stato i raggiunto dall'automa P (ciclo aperto) e lo stato j raggiunto dall'automa S (supervisore) dopo la sequenza di eventi w.
La sequenza di eventi "abcbc" conduce l'automa S/P nello stato x2,2.
In questo stato l'evento "c" (non controllabile) è disabilitato dal supervisore.
Nel corrispondente stato x2 dell'automa P l'evento "c" è attivo.
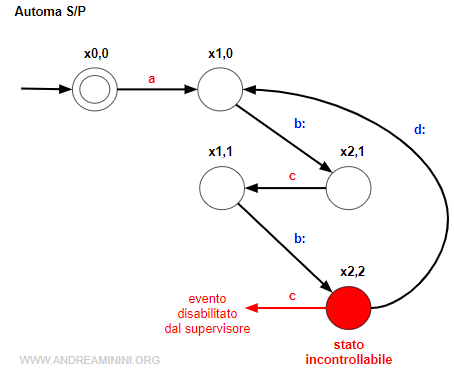
Questo vuol dire che il supervisore S non è abilitante rispetto a P e il linguaggio K non è controllabile.
Quindi, non posso usare il supervisore per applicare la specifica perché genera uno stato incontrollabile in x2,2.
Nota. Per risolvere il problema basta riscrivere la specifica K in modo che l'automa S supervisore non disabiliti l'evento "c". Una possibile soluzione è ridurre l'insieme degli eventi dell'automa da E'={b,d,c} a E'={b,d}, in questo modo l'insieme E' è composto solo da eventi controllabili. Questo sottolinguaggio è detto sottolinguaggio supremo. Dopo questa riduzione la specifica diventa controllabile.
Il sottolinguaggio controllabile supremo
Una specifica incontrollabile K potrebbe essere controllabile in un sottoinsieme K' in K.
Pertanto, se una specifica è incontrollabile, posso sempre provare a ridurre il linguaggio.
In questo modo ottengo un sottolinguaggio più restrittivo che genera meno parole legali.
Nota. In teoria ogni linguaggio include un sottolinguaggio controllabile ma non è detto che sia utile. Ad esempio, ogni linguaggio ha un sottolinguaggio vuoto {ε} controllabile ma non serve a nulla.
In genere, ogni linguaggio ha più sottolinguaggi controllabili.
Tra questi scelgo il sottolinguaggio meno restrittivo detto sottolinguaggio controllabile superemo KS.
$$ L'(S/P) = L(G) || K_s $$
Come si trova il sottolinguaggio supremo?
Una procedura è la seguente
- Elimino gli stati incontrollabili dell'automa S/P a ciclo chiuso.
- Elimino le transizioni che entrano ed escono dagli stati incontrollabili.
Il risultato finale è un linguaggio L'(S/P) uguale alla composizione concorrente L(G) || K_s.
Un esempio pratico
La specifica K causa uno stato incontrollabile in x2,2

Elimino lo stato x2,2 e le sue transizioni in entrata e in uscita.
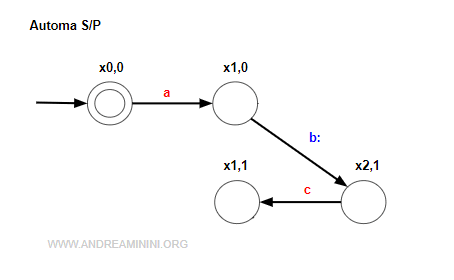
Questo sottolinguaggio K' è controllabile.
Non è detto però che sia anche utile.
E così via.
