Limitatezza della rete di Petri
In una rete di Petri devo distinguere tra due tipi di limitatizza relativi al singolo posto o all'intera rete.
Come capire se una rete è limitata? Per studiare la limitatezza della rete di Petri è sufficiente osservare il grafo di copertura. Se nessun posto ha il simbolo ω allora la rete è limitata.
Il posto k-limitato
Un posto p della rete è k-limitato se per ogni marcatura raggiungibile M di R(N,M0) si ha M(p)≤k, ossia il posto può ricevere/ospitare al massimo k marche.
Se un posto è limitato, nel grafo di copertura il posto non assume mai un numero superiore a k, né il simbolo ω.
Un posto limitato è detto sano (o binario) se può ricevere al massimo una marca ossia se è 1-limitato.
E' soltanto detto nodo limitato se k>1.
Nota. Va da sé che se il posto è k-limitato allora per ogni n>k è n-limitato.
Un esempio 1
Il posto p1 della rete è limitato perché può ospitare al massimo una marca.
Essendo 1-limitato, il posto è detto sano (o binario).
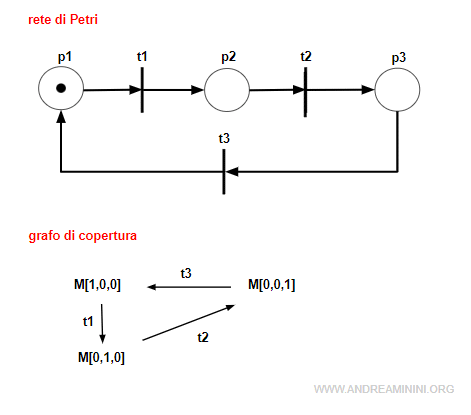
Nota. In questo esempio anche i posti p2 e p3 sono limitati perché possono ospitare al massimo una marca.
Esempio 2
In questa rete il posto p2 è 2-limitato perché può ricevere al massimo due marche contemporaneamente.
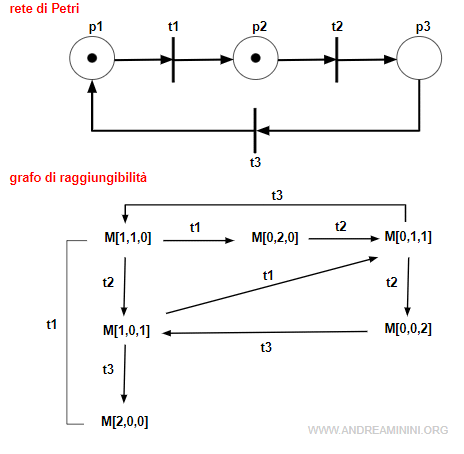
La rete k-limitata
Una rete marcata <N,M0> è detta k-limitata se ogni suo posto è k-limitato.
Quando una rete è limitata, il grafo di copertura non contiene il simbolo ω. Pertanto, è un grafo di raggiungibilità.
Una rete limitata è detta sana (o binaria) se è 1-limitata.
E' soltanto detta rete limitata se k>1.
Nota. Anche in questo caso è ovvio che se la rete è k-limitata allora per ogni n>k è n-limitata.
Esempio 1
Questa rete è limitata perché ogni posto è limitato.
Essendo ogni posto 1-limitato, la rete è detta sana.
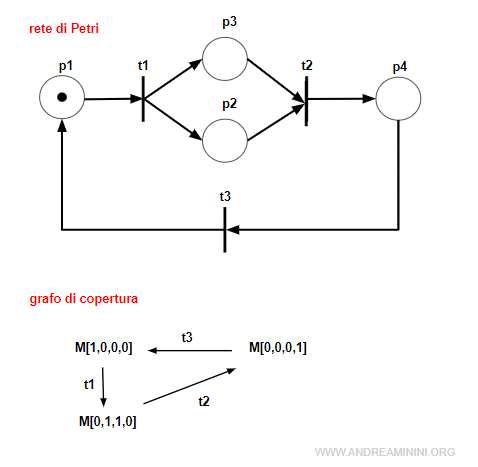
Nota. Una rete è detta sana anche se ci sono contemporaneamente due marche nel caso della marcatura raggiungibile M[0,1,1,0]. L'importante è che ci sia sempre non più di una marca per posto. In caso contrario non sarebbe sana ma soltanto limitata.
Esempio 2
Questa rete è limitata perché ogni posto può ricevere al massimo k=2 marche.
Pertanto, è una rete 2-limitata.
Esempio 2
In questa rete il posto p2 è 2-limitato perché può ricevere al massimo due marche contemporaneamente.

Il posto illimitato
Un posto è illimitato se può ricevere infinite marche.
Un esempio pratico
In questa rete il posto p3 è illimitato perché può ricevere infinite marche.
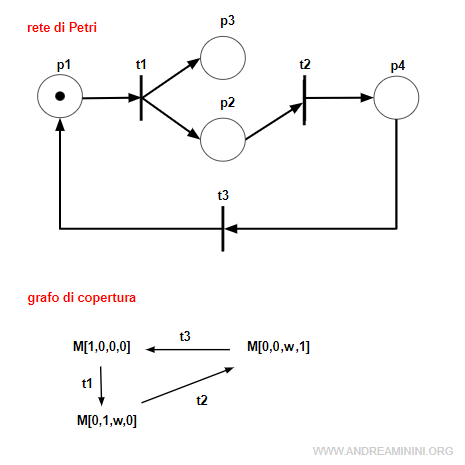
La rete illimitata
La rete è illimitata se almeno un suo posto è illimitato.
Un esempio pratico
Questa rete di Petri è illimitata perché il posto p3 è illimitato.
Gli altri posti p1 e p2 sono invece limitati ma non sono sufficienti a rendere limitata l'intera rete.

Teoremi sulla limitatezza
Finitezza dell'insieme di raggiungibilità
Una rete marcata <N,M0> è limitata se e solo se il suo insieme di raggiungibilità R(N,M0) è finito.
Dimostrazione
Prendo in considerazione una rete con p posti.
Se l'insieme di raggiungibilità della rete è finito, osservando tutte le marcature raggiungibili M posso trovare il posto che ottiene più marcature M(p) rispetto agli altri.
$$ k = max(M(p)) \forall M \in R(N,M_0) $$
Essendo k un numero finito, la rete è sicuramente k-limitata.
Creo un vettore composto da p elementi e a ciascun elemento assegno il valore k
$$ k' = [a_1, a_2, a_3, ... , a_p] = [ k, k, k, .... , k ] $$
A partire da questo vettore creo un insieme K composto da tutte le possibili combinazioni k x k x k ... x k
$$ K = { [0,0,0,...], [0,0,1,...], [0,0,2,...], ... , [k,k,...,k-1], [k,k,...,k] } $$
Essendo k un numero finito anche l'insieme K è un insieme finito ossia composto da kp elementi.
Poiché l'insieme di raggiungibilità R(N,M0) è un sottoinsieme di K.
$$ R(N,M_0) ⊆ K $$
Ne deduco che anche l'insieme di raggiungibilità è un insieme finito.
Esempio
Questa rete ha p=3 posti ed è 2-limitata.

L'insieme di raggiungibilità R(N,M0) è composto dalle marcature raggiungibili
$$ M[1,1,0] \\ M[0,2,0] \\ M[0,1,1] \\ M[1,0,1] \\ M[0,0,2] \\ M[2,0,0] $$
Il numero di marche più alto in ogni posto della rete è k = 2.
Creo il vettore k' con elementi uguali a k=2.
$$ k' = [2,2,2] $$
Il vettore appartiene all'insieme K composto da ogni possibile combinazione 2x2x2 ossia da 23=8 elementi
$$ K = { [0,0,0], [0,0,1], [0,0,2], ... , [2,2,1], [2,2,0] } $$
Essendo k=2 un numero finito anche l'insieme K è un insieme finito.
E' evidente che l'insieme R(N,M0) è un sottoinsieme di K
$$ R(N, M_0) ⊆ K $$
Se K è un insieme finito allora anche i suoi sottoinsiemi sono finiti.
Pertanto, l'insieme di raggiungibilità R(N,M0) è un insieme finito.
E così via.
