Rete di petri ripetitiva

Cos'è una rete ripetitiva

Una rete marcata <N,M₀> è detta rete ripetitiva se esiste una sequenza di transizioni σ ripetitiva.

Una sequenza di transizioni non vuota σ è detta ripetitiva se si ripete un numero infinito di volte a partire da una marcatura abilitante M.

$$ M[σ \:>\: M_1[σ \:>\: M_2[σ \:>\: ... $$

Attenzione. La rete di Petri è detta ripetitiva solo se si ripete infinite volte. Se la sequenza si ripete soltanto per un numero determinato di volte, la rete non è una rete ripetitiva. Pertanto, con l'iterazione il numero delle marche nella rete ripetitiva non dimunuisce mai. Può restare costante o aumentare. $$ M[σ \:>\: M' \:\:\: con \:\:\: M' \ge M $$

Un esempio pratico

Esempio 1

Questa rete è ripetitiva perché contiene alcune sequenze che possono ripetersi all'infinito.

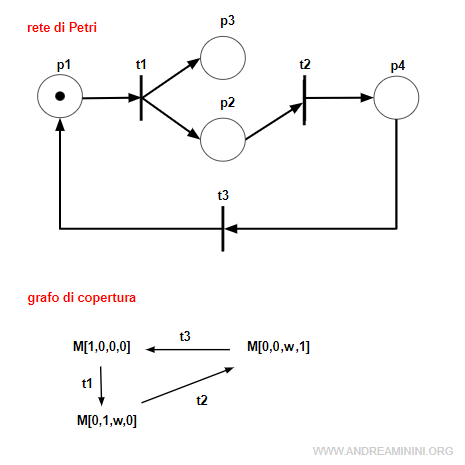
Sono sequenze ripetute

• la sequenza σ=t₁t₂t₃ a partire da M[1,0,0,0]
• la sequenza σ=t₂t₃t₁ a partire da M[0,1,0,0]
• la sequenza σ=t₃t₁t₂ a partire da M[0,0,1,0]

La sequenza ripetitiva stazionaria o crescente

Esistono due tipologie di sequenze ripetitive:

• La sequenza stazionaria
  Una sequenza di transizioni ripetitiva è detta stazionaria se è abilitata dalla stessa marcatura M $$ M[σ \:>\: M $$ Nella sequenza stazionaria il numero delle marche è costante.
  

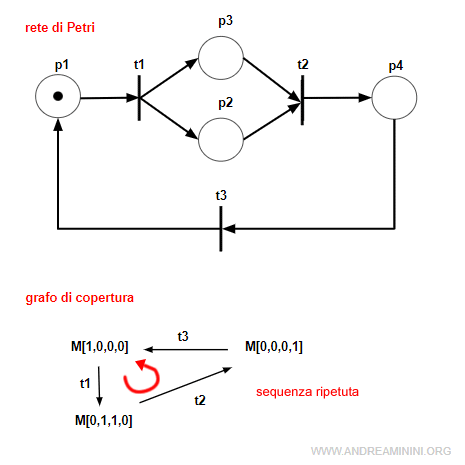
  Nota. La sequenza stazionaria può verificarsi sia in una rete limitata che illimitata.

• La sequenza crescente
  Una sequenza di transizioni ripetitiva è detta crescente se è abilitata da marcature con un numero di marche crescenti. $$ M[σ \:>\: M' \:\: con \:\: M'>M $$ Nella sequenza crescente il numero delle marche aumenta dopo ogni iterazione.
  

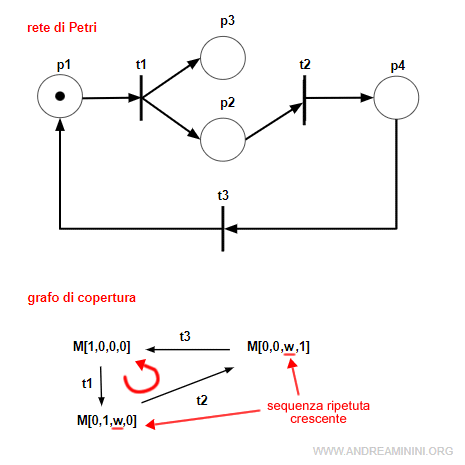
  Nota. La presenza di una sequenza crescente si presenta soltanto se la rete è illimitata. Quindi, una rete marcata è limitata soltanto se e solo se non ammette sequenze ripetitive crescenti.

L'analisi del grafo di raggiungibilità

La ripetitività della rete si può constatare osservando il grafo di raggiungibilità.

Se la rete è ripetitiva, esiste un ciclo orientato nel grafo di raggiungibilità con gli archi che formano la sequenza ripetuta.

Un esempio pratico

In questa rete si può facilmente notare la presenza di un ciclo in corrispondenza della sequenza ripetuta σ=t₁t₂t₃.

Osservando il ciclo nel grafo orientato si può capire se la sequenza è stazionaria o crescente.

• Sequenza stazionaria
  La sequenza è stazionaria se le marcature del ciclo non presentano il simbolo ω.
• Sequenza crescente
  La sequenza è crescente se le marcature del ciclo presentano il simbolo ω.

  Esempio. Questa sequenza ripetuta è crescente perché il numero delle marche aumenta dopo ogni iterazione. Nel ciclo è presente il simbolo ω nel posto p₃.
  

E' una delle condizioni necessarie per verificare la ripetitività e la stazionarietà di una rete.

E così via.