Memoria di abilitazione e memoria totale
Negli automi DFA temporizzati posso usare due tipologie di memorie.
- La memoria di abilitazione
Azzera il valore dell'orologio di un evento quando l'evento viene disabilitato. Alla riattivazione, l'orologio dell'evento assume il valore di default, secondo la sequenza stabilita nella struttura di temporizzazione. $$ o'_e = \begin{cases} o_e - o* \:\:\: se \:\: e \ne e' \:∧ \: e \in A(x) \\ θ_{e,v_e+1} \:\:\: altri \: casi \end{cases} $$ - La memoria totale
Tiene traccia del valore dell'orologio di un evento quando viene disabilitato. Alla riattivazione, l'orologio ha il valore precedente. In pratica, l'orologio viene congelato (hold) fino alla successiva riattivazione. $$ o'_e = \begin{cases} o_e - o* \:\:\: se \:\: e \ne e' \:∧ \: e \in A(x) \\ θ_{e,v_e+1} \:\:\: se \:\: e = e' \\ o_e \:\:\: altri \: casi \end{cases} $$
Nota. La variabile oe è l'orologio dell'evento e ossia il tempo che manca al suo verificarsi. La variabile o* è il tempo rimanente al successivo evento (di qualsiasi tipo). L'evento e' è l'evento successivo. L'orologio o'e è l'aggiornamento dell'orologio dell'evento e. La variabile θ è la struttura della temporizzazione degli eventi.
Un esempio pratico
L'automa di una macchina non affidabile si basa su tre stati: spegnimento (F), lavoro(L), guasto(G).
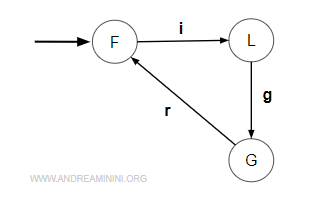
Quindi lo spazio degli stati è
$$ X=\{ F,L,G \} $$
Nello stato iniziale la macchina si trova nello stato F
$$ x_0= F $$
Ci sono tre eventi possibili: inizio(i), fine(f), rottura(g), riparazione(r).
$$ E=\{ i,f,g,r \} $$
Le transizioni possibili sono le seguenti:
$$ δ(x,i)=L \\ δ(x,f)=F \\ δ(x,g)=G \\ δ(x,r)=F $$
Gli eventi attivi sono
$$ A(F)=\{ i \} \\ A(L) = \{ f,g \} \\ A(G)= \{ r \} $$
La struttura di temporizzazione θ è composta dai seguenti orologi.
$$ θ_i=1 \\ θ_f=2 \\ θ_g=5 \\ θ_r=2 $$
Ora confronto il comportamento di un automa con memoria di abilitazione e con memoria totale.
Nota. Gli automi con memoria di abilitazione e con memoria totale sono identici nella funzione di transizione, nello spazio degli stati e degli eventi. Cambia soltanto la struttura di temporizzazione degli orologi. Nel primo caso la disabilitazione azzera l'orologio mentre nel secondo caso ne sospende temporaneamente per riprenderlo alla successiva attivazione dell'evento.
1] Automa con memoria di abilitazione
In questo caso l'automa non abilita mai l'evento (g) perché l'orologio Og si resetta a zero ogni volta che l'evento di rottura (g) viene disabilitato.
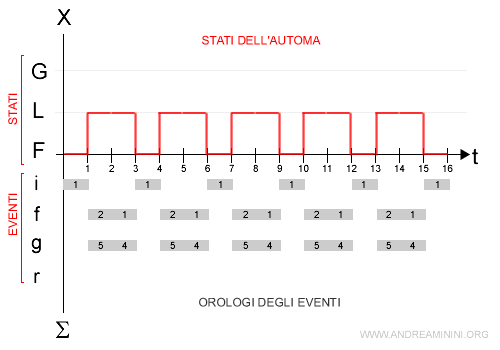
Lo stato guasto (G) non viene mai raggiunto perché l'evento (g) non viene mai abilitato.
Conseguentemente anche lo stato di riparazione (r) non viene mai abilitato.
Spiegazione. Nell'iterazione t=1 l'automa entra nello stato L e abilita per la prima volta l'evento (g) in quanto è incluso negli eventi attivi A(L)={f,g} dello stato L. All'orologio dell'evento (g) viene assegnato il valore iniziale θg=5. Nell'iterazione t=3 l'automa termina la lavorazione e torna allo stato F. L'evento (g) viene disabilitato perché non è incluso negli spazi attivi A(F) dello stato F. L'orologio o(g) vale 3 ma viene azzerato con la disabilitazione e ricomincia il conteggio da θg=5 quando, nell'iterazione t=4, l'automa ritorna nello stato L.
2] Automa con memoria totale
In questo caso l'automa abilita l'evento (g) dopo 5 step, perché l'orologio Og è soltanto congelato durante le fasi in cui l'evento (g) è disabilitato, ossia conserva il suo valore.
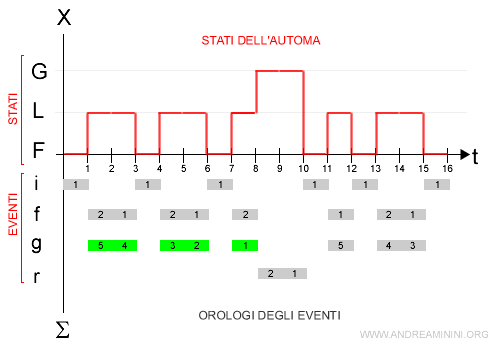
Lo stato guasto (G) viene raggiunto dopo cinque iterazioni.
Altre due iterazioni sono necessarie per l'evento di riparazione (r).
Spiegazione. Nell'iterazione t=1 l'automa passa dallo stato F allo stato L dove abilita l'evento (g) in quanto è incluso negli eventi attivi A(L)={f,g} dello stato L. All'orologio dell'evento (g) è assegnato il valore iniziale θg=5. Nell'iterazione t=3 l'automa conclude la lavorazione e torna allo stato F. L'evento (g) viene disabilitato perché non è incluso negli spazi attivi A(F) dello stato F. L'orologio o(g) vale 3 e non viene azzerato con la disabilitazione. In questo caso, l'orologio o(g) ricomincia il conteggio da 3 quando, nell'iterazione t=4, l'automa ritorna nello stato L. Nell'iterazione t=8 l'orologio o(g)=0 e l'automa esegue l'evento g spostandosi dallo spazio L allo spazio G (guasto) dove resta per due iterazioni, il tempo necessario per eseguire l'evento (r) della riparazione e tornare nello stato F.
E così via.
