Il comportamento a regime di una catena di Markov
Una catena di Markov raggiunge la condizione a regime quando le probabilità di stato si assestano a valori costanti.
Questa condizione di equilibrio viene raggiunta dal sistema dopo molte iterazioni.
Tuttavia, non è detto che esista sempre.
Nota. Per verificare a priori la sua esistenza posso calcolare il limite delle probabilità. Se esistono dei valori asintotici, esiste anche la distribuzione di stato a regime. $$ π_j = \lim_{k \rightarrow \inf } π_j(k) $$
La catena ergodica
La catena di Markov è detta ergodica se i limiti di probabilità πj $$ \lim_{k \rightarrow ∞ } π_j (k) $$ che compongono la distribuzione limite delle probabilità a regime $$ π = [ π_0,π_1, ... ] $$ esistono per ogni xj e sono indipendenti dal vettore iniziale π(0)
Nella catena ergodica il vettore della distribuzione limite delle probabilità degli stati a regime
$$ π = [ π_0,π_1, ... ] $$
equivale a trovare una soluzione al seguente sistema di equazioni
$$ \begin{cases} π=πP \\ sum_{x_j \in X} π_j = 1 \end{cases} $$
Pertanto, lo studio del comportamento a regime ha significato soltanto se la catena è ergodica.
Nota. Una catena ergodica è irriducibile.
Come riconoscere una catena ergodica
Esistono diversi metodi.
- Metodo degli autovalori
La matrice stocastica di una catena ergodica omogenea e finita ha gli autovalori con modulo minore di 1 ad eccezione dell'autovalore uguale a 1. - Metodo grafico
Il grafo di una catena ergodica omogenea e finita ha un solo nodo assorbente (terminale). Il nodo assorbente è aperiodico.
Un esempio pratico
Prendo come esempio una catena di Markov
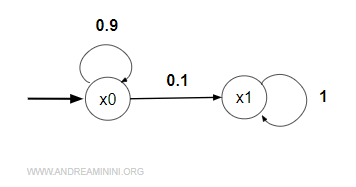
Nota. La catena ha uno stato transiente (x0) e uno stato assorbente (x1) aperiodico. E' quindi evidente che si tratti di una matrice ergodica ( metodo grafico ).
con questa matrice delle probabilità di transizione
$$ P \begin{pmatrix} 0.9 & 0.1 \\ 0 & 1 \end{pmatrix} $$
Nota. Gli autovalori della matrice sono λ1=0.9 e λ2=1. E' una matrice ergodica perché esiste un solo autovalore uguale a 1 e il modulo degli altri è minore di 1 ( metodo degli autovalori ).
Analizzo l'evoluzione negli stati successivi
$$ P^2 = \begin{pmatrix} 0.9^2 & 0.9 \cdot 0.1 + 0.1 \\ 0 & 1 \end{pmatrix} $$
$$ P^3 = \begin{pmatrix} 0.9^3 & 0.9^2 \cdot 0.1 + 0.9 \cdot 0.1 + 0.1 \\ 0 & 1 \end{pmatrix} $$
$$ P^k = \begin{pmatrix} 0.9^k & 0.1 \cdot \sum_{i=0}^{k-1} 0.9^i \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 0.9^k & 1-0.9^k \\ 0 & 1 \end{pmatrix} $$
La probabilità iniziale è
$$ π(0) = \{ π_1 , π_2 \} $$
La probabilità all'istante k è
$$ π(k) = π(0) P^k = \{ 0.9^k \cdot π_1, π_1+π_2-0.9^k \cdot π_1 \} $$
Il limite per k che tende a infinito è
$$ \lim_{k \rightarrow ∞ } π(k) $$
$$ \lim_{k \rightarrow ∞ } \{ 0.9^k \cdot π_1, π_1+π_2-0.9^k \cdot π_1 \} = \{ 0, π_1+π_2 \} = \{ 0, 1 \} $$
La distribuzione limite della matrice ergodica coincide con la distribuzione stazionaria.
E così via.
