Equazione di Chapman-Kolmogorov

L'equazione di Chapman-Kolmogorov è un'equazione di evoluzione delle catene di Markov a tempo discreto che permette di calcolare la probabilità di uno stato all'istante k. $$ p_{ij} (k,k+n) = \sum_{r \in X} p_{ir}(k,h) \cdot p_{rj} (h,k+n) $$ oppure in forma matriciale $$ P(k,k+n) = P(k+h) \cdot P(h,k+n) $$ con k ≤ h ≤ k+n

Un processo per passare dallo stato i allo stato j deve passare per qualche stato intermedio.

Nota. E' un metodo più efficiente per calcolare la probabilità di uno stato dopo k passi rispetto al calcolo delle k-1 matrici di transizione. $$ π(k) = π(0) \cdot P(0) \cdot P(1) \cdot \cdot \cdot P(k-1) $$

Dimostrazione e spiegazione

La probabilità di trovarsi in uno stato x_j dopo n transizioni a partire da uno stato iniziale x_i è

$$ p_{ij} (k,k+n) = P\{ x(k+n) | x(k) \} = P\{ x_j | x_i \} $$

Dove k sono le transizioni passate che hanno portato l'automa allo stato x_i. Potrebbe anche essere k=0 se x_i è lo stato iniziale dell'automa.

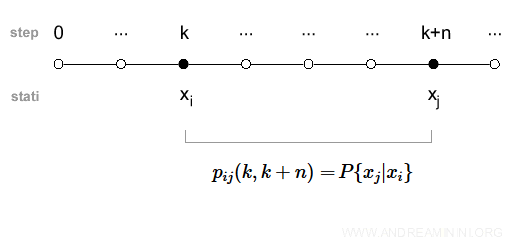
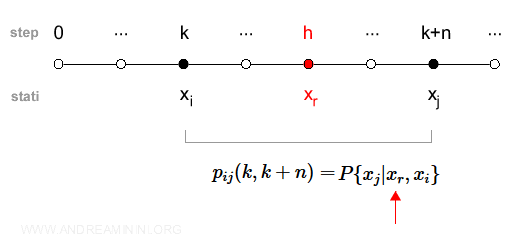
Posso calcolare la probabilità in ogni singolo passo intermedio (h) tra k e k+n.

$$ p_{ij} (k,k+n) = P\{ x(k+n) | x(h), x(k) \} = P\{ x_j | x_r, x_i \} $$

Dove h è il passo intermedio k≤h≤k+n e x_r è lo stato intermedio al passo h.

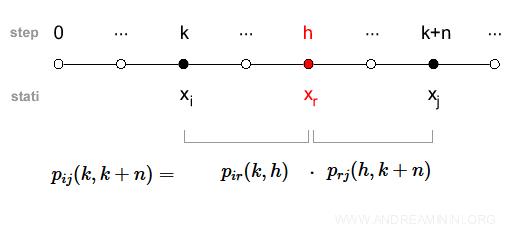
Pertanto, la probabilità totale di arrivare a x_j da x_i è pari alla somma delle probabilità di passare per ciascun stato intermedio x_r.

$$ p_{ij} (k,k+n) = \sum_{r \in X} p_{ir}(k,h) \cdot p_{rj} (h,k+n) $$

Dove p_ir è la probabilità di arrivare a x_r da x_i dopo h passi, mentre p_ir è la probabilità di arrivare a x_j da x_r dopo k+n passi dall'inizio.

Nota. Nella formula di Chapman-Kolmogorov c'è una sommatoria perché l'automa potrebbe passare per diversi stati intermedi x_r dopo h passi. Non è detto che ci sia un solo stato intermedio x_r dopo h passi. Quindi, vanno considerate tutte le probabilità di passaggio per gli stati intermedi alternativi. Ad esempio, se devo calcolare la probabilità di passare da x0 a x4 dopo h=2 passi devo considerare due cammini alternativi possibili: x0-x1-x3 e x0-x2-x3.

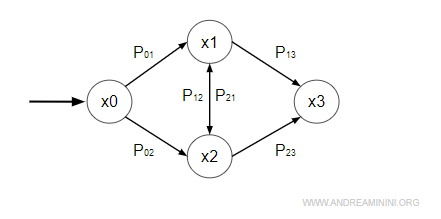
Pertanto, la probabilità di arrivare a x3 da x0 in h=2 passi (con k=0) è la somma delle probabilità di entrambi i cammini $$ p_{0,3} = ( p_{0,1} \cdot p_{1,3} ) + ( p_{0,2} \cdot p_{2,3} ) $$

Considerando che l'insieme delle probabilità pij da k a k+n compone la matrice di transizione P

$$ P(k,k+n) = [ p_{ik}(k+k+n)] $$

L'equazione di Chapman-Kolmogorov

$$ p_{ij} (k,k+n) = \sum_{r \in X} p_{ir}(k,h) \cdot p_{rj} (h,k+n) $$

può essere usata per costruire la matrice di transizione P a n passi

$$ P(k,k+n) = P(k,h) \cdot P(h,k+n) $$

A seconda dell'elemento intermedio h posso creare diverse versioni dell'equazione di Chapman-Kolmogorov in forma matriciale. In particolar modo le seguenti:

• Forward ( in avanti )
  Se lo stato intermedio è il penultimo, ossia quello che precede lo stato k+n. $$ h=k+n-1 $$
• Backward ( all'indietro )
  Se lo stato intermedio è il secondo del cammino, ossia quello che segue lo stato k $$ h=k+1 $$

Nota. Se la catena di Markov a tempo discreto ha una matrice di transizione omogenea posso usare una versione semplificata dell'equazione di Chapman-Kolmogorov. E' consigliabile perché è molto più rapida e facile da calcolare.

L'equazione di Chapman-Kolmogorov per le matrici omogenee

Esiste anche una versione semplificata dell'equazione di Chapman-Kolmogorov che si applica soltanto per le matrici stocastiche di transizione omogenee.

$$ π(k) = π(0)P^{k} $$

Questa formula è molto utile perché consente di calcolare con pochi passaggi la probabilità π(k) di trovarsi in uno stato dopo k passi, direttamente dalle probabilità dello stato iniziale π(0).

Cos'è una matrice stocastica omogenea. Una matrice di transizione è omogenea se è tempoinvariante. Le probabilità di transizione di stato non dipendono dall'istante k. Le probabilità di transizione sono costanti. E' una delle situazioni più frequenti nell'analisi di un automa.

Dimostrazione

Una matrice omogenea P è indipendente dal tempo k (tempoinvariante).

I valori P(0), P(1), ... , P(k-1) sono tutti uguali a P

$$ π(k) = π(0) \cdot P(0) \cdot P(1) \cdot \cdot \cdot P(k-1) $$

$$ π(k) = π(0) \cdot P^{k} $$

Quindi posso sostituire P(k) con P anche nell'equazione di evoluzione

$$ π(k+1) = π(k)P(k) $$

$$ π(k+1) = π(k)P $$

che posso riscrivere nella seguente forma

$$ π(k+1) = π(0)P^{k+1} $$

ossia più in generale

$$ π(k) = π(0)P^{k} $$

Nota. La probabilità di trovarsi in uno stato dopo k passi è in funzione delle probabilità precedenti. Quindi, è in funzione di π(0) perché è l'unico valore indipendente che determina tutti gli altri. $$ π(k) = π(0) \cdot P(0) \cdot P(1) \cdot \cdot \cdot P(k-1) $$ Ad esempio la probabilità di trovarsi in uno stato x dopo k=1 passi è $$ π(1) = π(0) \cdot P $$ Quindi, la probabilità di trovarsi nel successivo passo k+1=2 è $$ π(2) = π(1) \cdot P = [ π(0) \cdot P ] \cdot P = π(0) \cdot P^2 $$ e in generale la probabilità di trovarsi nel k-esimo passo successivo $$ π(k) = π(0) \cdot P^{k} $$

L'equazione di transizione a n stati di Chapman-Kolmogorov diventa

$$ P(n) = P^{n-h} \cdot P^h $$

Quindi, nel caso delle matrici omogenee le formule backward e forward di Chapman-Kolmogorov coincidono

• Forward ( in avanti )
  Essendo h=k+n-1 con k=0 diventa h=n-1.
  $$ P(n) = P^{n-h} \cdot P^h = P^{n-(n-1)} \cdot P^{n-1} = P \cdot P^{n-1} $$
• Forward ( in avanti )
  Essendo h=k+1 con k=0 diventa h=1.
  $$ P(n) = P^{n-h} \cdot P^h = P^{n-1} \cdot P^{1} = P^{n-1} \cdot P $$

Un esempio pratico

Un automa ha due stati x₀ e x₁.

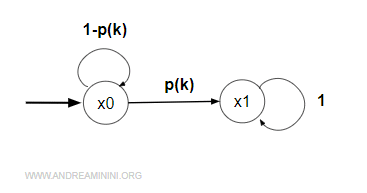
La probabilità di transitare da x₀ a x₁ è 0.20.

$$ p(k)=0.20 $$

Quindi, la matrice delle probabilità di transizione è

$$ P = \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} $$

La probabilità assoluta iniziale perché lo stato iniziale è x₀.

$$ π(0) = \{ 1 , 0 \} $$

La probabilità di transizione all'istante k=1 è

$$ π(1) = π(0) \cdot P $$

$$ π(1) = \{ 1 , 0 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} = \{ 0.20 , 0.80 \} $$

La probabilità di transizione all'istante k=2 è

$$ π(2) = π(0) \cdot P^2 $$

$$ π(2) = \{ 1 , 0 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix}^2 $$

$$ π(2) = \{ 1 , 0 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} $$

$$ π(2) = \{ 0.20 , 0.80 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} = \{ 0.04 , 0.96 \} $$

La probabilità di transizione all'istante k=3 è

$$ π(3) = π(0) \cdot P^3 $$

$$ π(3) = \{ 1 , 0 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix}^3 $$

$$ π(3) = \{ 1 , 0 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix}^2 \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} $$

$$ π(3) = \{ 0.04 , 0.96 \} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} = \{ 0.008 , 0.992 \} $$

Nota. In questo modo è decisamente più facile calcolare la transizione a n passi di una catena di Markov a tempo discreto rispetto al metodo tradizionale. $$ π(k) = π(0) \cdot P(0) \cdot P(1) \cdot \cdot \cdot P(k-1) $$

E così via.