La differenza tra espressioni regolari e automi
Le espressioni regolari e gli automi deterministici (DFA) e non deterministici (NFA) sono classi di linguaggi differenti.
Qual è la differenza?
Le espressioni regolari usano dei linguaggi regolari. Gli automi, invece, soltanto il linguaggio accettato da un DFA o NFA.
Tuttavia, è possibile dimostrare l'equivalenza tra le tre classi di linguaggio.
$$ L_{ER} = L_{DFA} = L_{NFA} $$
Per dimostrare l'uguaglianza delle espressioni regolari è sufficiente dimostrare che
$$ L_{DFA} ⊆ L_{ER} ⊆ L_{NFA} $$
Sapendo che gli automi LDFA e LNFA sono equivalenti tra loro, da questo si deduce l'equivalenza tra la classe delle espressioni regolari e le classi degli automi DFA e NFA.
Equivalenza tra DFA ed espressioni regolari
La classe dei linguaggi regolari comprende la classe dei linguaggi accettati da un automa DFA.
Data un'espressione regolare qualsiasi a posso individuare un automa deterministico a stati finiti G ossia un automa DFA
$$ L(a)=L_m(G) $$
Come funziona?
A ogni stato xi dell'automa DFA associo un'espressione regolare αi che descrive il linguaggio generato dall'automa dallo stato iniziale x0 fino allo stato xi.
Qualsiasi stato dell'automa xi è raggiungibile con k transizioni di stato.
$$ x_i = δ(x_0,e_1) + δ(x_1,e_2) + ... + δ(x_k,e_{k+1}) $$
Poiché ogni stato x_i è raggiungibile da un'espressione regolare alfa, posso riscrivere la precedente sotto forma di ER
$$ α_i = α_1e_1 + α_2+e_2+...+α_ke_k $$
Nota. Ogni espressione regolare a_k indica l'ER necessaria per raggiungere lo stato xk a partire dallo stato iniziale x0.
Considerando anche una e-transizione iniziale e un cappio sullo stato terminale, l'espressione diventa
$$ α_i = ε + α_1e_1 + α_2+e_2+...+α_ke_k + α_je_j$$
Questa premessa mi permette di capire l'algoritmo per trovare l'espressione regolare di un automa DFA.
Come trovare le espressioni regolari di un automa deterministico
Posso trasformare un automa DFA in un'espressione regolare ER usando questa procedura.
- Associo a ogni i-esimo stato dell'automa G una espressione regolare ai
- Risolvo il sistema di equazioni
- La somma delle espressioni regolari degli stati xi ∈ X è uguale al linguaggio generato dall'automa G $$ L(G) = \sum a_x $$
- La somma delle espressioni regolari degli stati terminali xi ∈ Xm è uguale al linguaggio accettato dall'automa $$ L_m(G) = \sum a_xm $$
Un esempio pratico
Devo trovare l'espressione regolare di questo automa DFA.
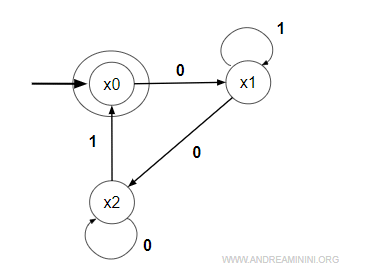
Lo stato iniziale x0 è anche lo stato finale.
Non ci sono altri stati finali, quindi l'insieme Xm degli stati terminali è composto solo da x0.
$$ X_m = \{ x_0 \} $$
Assegno a ogni stato un'espressione regolare α.
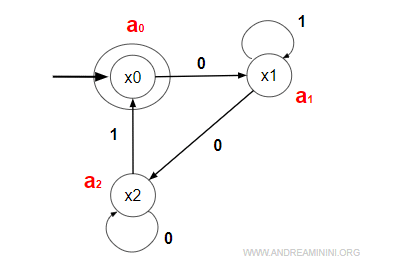
Poi definisco le espressioni regolari per ciascun stato:
$$ \begin{cases} a_0 = ε + a_21 \\ a_1 = a_00+a_11 \\ a_2=a_10+a_20 \end{cases} $$
La terza espressione regolare può essere trasformata in a2=a100*
Nota. Date tre espressioni regolari a,b,c in combinazione tra loro. $$ a= b + ac $$ equivale a $$ a=bc* $$ Quindi, nell'espressione a2=a10+a20 le componenti sono β=a10 e γ=0. Quindi, a2=a10·0*. 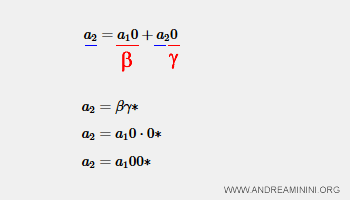
Quindi il sistema diventa
$$ \begin{cases} a_0 = ε + a_21 \\ a_1 = a_00+a_11 \\ a_2=a_100* \end{cases} $$
Poi sostituisco a2 nella prima equazione
$$ \begin{cases} a_0 = ε + (a_100*)1 \\ a_1 = a_00+a_11 \\ a_2=a_100* \end{cases} $$
La terza equazione posso riscriverla in a1=a001* usando la formula a=b+c=bc*
$$ \begin{cases} a_0 = ε + (a_100*)1 \\ a_1 = a_001* \\ a_2=a_100* \end{cases} $$
A questo punto sostituisco a1 nella prima e nella terza equazione.
$$ \begin{cases} a_0 = ε + ((a_001*)00*)1 \\ a_1 = a_001* \\ a_2=(a_001*)00* \end{cases} $$
$$ \begin{cases} a_0 = ε + (a_001*00*1) \\ a_1 = a_001* \\ a_2=a_001*00* \end{cases} $$
La prima equazione posso riscriverla in a0=(01*00*1)* usando la formula a=b+c=bc*
$$ \begin{cases} a_0 = (01*00*1)* \\ a_1 = a_001* \\ a_2=a_001*00* \end{cases} $$
Sostituisco a0 nelle altre equazioni
$$ \begin{cases} a_0 = (01*00*1)* \\ a_1 = (01*00*1)*01* \\ a_2=(01*00*1)*01*00* \end{cases} $$
Il linguaggio generato L(G) dell'automa è la somma delle singole ER appena trovate
$$ L(G) = a_0 + a_1 + a_2 $$
$$ L(G) = (01*00*1)* + (01*00*1)*01* + (01*00*1)*01*00* $$
$$ L(G) = (01*00*1)* ( ε + 01* + 01*00* ) $$
Il linguaggio accettato Lm(G) dell'automa è uguale alla somma delle ER degli stati terminali.
In questo caso, c'è un solo stato terminale ossia x0.
$$ L(G) = a_0 = (01*00*1)* $$
Ho trovato le espressioni regolari equivalenti al linguaggio generato L(G) e accettato Lm(G) dell'automa DFA.
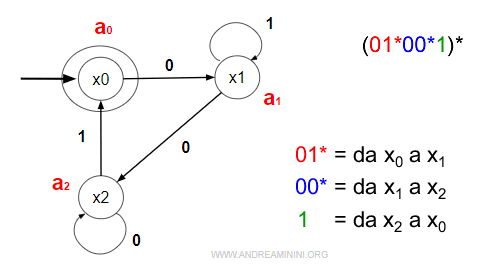
Nota. L'operatore * equivale a un ciclo completo nel digrafo in cui dopo una sequenza di eventi (parola) l'automa ritorna allo stesso stato di partenza. Ad esempio, l'espressione (01∗00∗1)∗ parte dallo stato x0 e ritorna allo stato x0.
Equivalenza tra NFA ed espressioni regolari
La classe dei linguaggi accettati da un automa NFA include all'interno anche i linguaggi regolari.
Pertanto, qualsiasi espressione regolare è accettata da un automa NFA.
Dimostrazione
Secondo la definizione di linguaggio regolare
Dato un alfabeto E, un linguaggio regolare è un sottoinsieme E* ottenuto con operazioni di unione, concatenazione e stella di Kleen sui linguaggi 0, {ε} e {e}. Dove e indica ogni simbolo dell'alfabeto E.
Se il linguaggio L di un automa NFA include il linguaggio regolare dell'espressione regolare, allora include anche l'unione, la concatenazione e la stella di Kleen dei linguaggi accettati.
Dati due linguaggi accettati L' e L" da due atomi G' e G" nello stesso alfabeto E, esiste un automa non deterministico G che rispetta le seguenti proprietà:
- Ogni espressione regolare atomica α è accettata dall'automa G $$ L_m(G) = L_m(e) = \{ e \} $$
- L'automa G accetta l'unione dei linguaggi accettati dagli automi G' e G" $$ L_m(G) = L_m(G') ∪ L_m(G") $$
- L'automa G accetta la concatenazione dei linguaggi accettati dagli automi G' e G" $$ L_m(G) = L_m(G') L_m(G") $$
- L'automa G accetta la stella di Kleene dei linguaggi accettati dagli automi G' e G" $$ L_m(G) = L_m(G')* $$ $$ L_m(G) = L_m(G")* $$
Quindi, sull'alfabeto E l'automa G accetta un linguaggio regolare.
Questo dimostra che i linguaggi regolari sono inclusi nella classe dei linguaggi accettati dagli automi NFA.
E così via.
