Come trovare gli stati indistinguibili di un automa
Per trovare gli stati in un automa AFD posso usare l'algoritmo di Hopcroft
- Creo una tabella con tutte le combinazioni tra gli stati dell'automa. Poi la trasformo in triangolare per evitare i confronti duplicati
- Elimino le combinazioni in cui uno stato è finale e l'altro non è finale
- Elimino le combinazioni che hanno eventi (simboli) in uscita diversi
- Elimino le combinazioni la cui coppia { δ(xi,e) , δ(xj,e) } individua una combinazione già eliminata dalla tabella per almeno un evento (e).
- Le coppie rimanenti nella tabella sono gli stati indistinguibili dell'automa.
A cosa serve trovare gli stati indistinguibili? Gli stati indistinguibili possono essere accorpati tra loro riducendo al minimo il numero degli stati dell'automa senza comprometterne il linguaggio e l'efficacia.
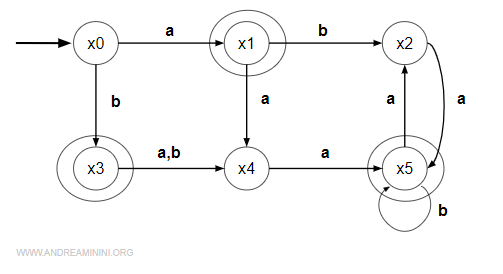
Un esempio pratico
Questo automa può essere ridotto. Per farlo occorre trovare gli stati indistiguibili.
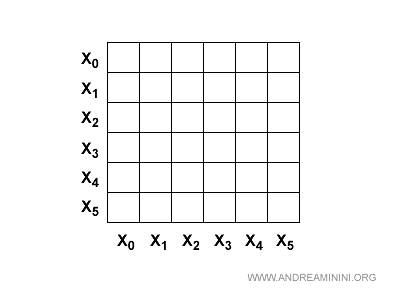
Creo la tabella delle combinazioni degli stati, ossia delle coppie (x,x') possibili.
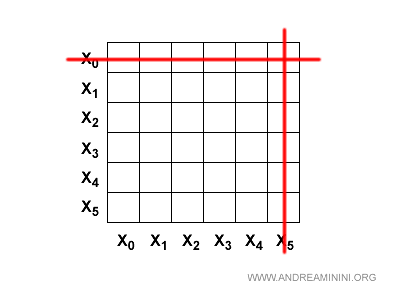
Elimino la prima riga e l'ultima colonna.
La trasformo in matrice triangolare per evitare i doppi confronti e i confronti tra gli stati per se stessi.
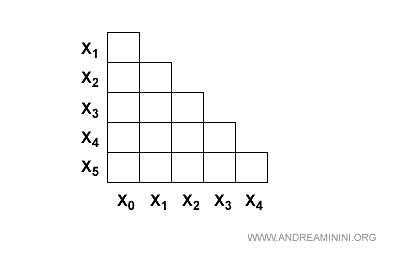
Elimino le combinazioni in cui uno stato è finale e l'altro no.
Sapendo che gli stati finali dell'automa sono Xm={x1,x3,x5}
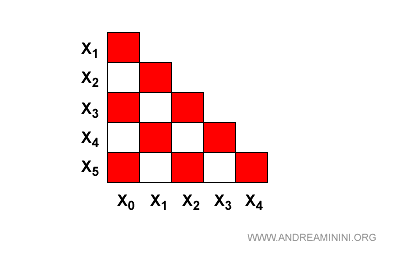
Poi elimino le coppie di stati che hanno eventi abilitanti diversi.
Per eventi abilitanti intendo i simboli che determinano le transizioni in uscita dallo stato in questione.
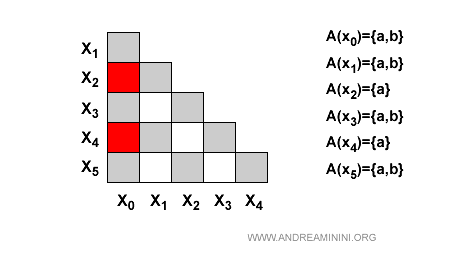
Nota. Soltanto le coppie (x0,x2) e (x0,x4) hanno eventi abilitanti diversi perché A(x2)={a} e A(x0)={a,b}. Lo stesso vale per il confronto tra x0 e x4. Le altre coppie hanno tutte gli stessi eventi abilitanti {a,b}.
Per le coppie restanti (caselle bianche) calcolo le accoppiate delle transizioni in uscita per ogni evento.
Se nel confronto almeno un'accoppiata corrisponde a una combinazione già eliminata, elimino la coppia.
Coppia x1,x3
$$ \begin{cases} δ(x_1,a)=x_4 \\ δ(x_3,a)=x_4 \end{cases} $$
La casella {x4,x4} non è marcata. E' un confronto diretto ed è fuori tabella.
$$ \begin{cases} δ(x_1,b)=x_4 \\ δ(x_3,b)=x_2 \end{cases} $$
La casella {x4,x2}={x2,x4} non è marcata.
Coppia x1,x5
$$ \begin{cases} δ(x_1,a)=x_4 \\ δ(x_5,a)=x_2 \end{cases} $$
La casella {x4,x2}={x2,x4} non è marcata.
$$ \begin{cases} δ(x_1,b)=x_4 \\ δ(x_5,b)=x_5 \end{cases} $$
La casella {x4,x4} è marcata.
Quindi la coppia confrontata {x1,x5} va eliminata dalla tabella.
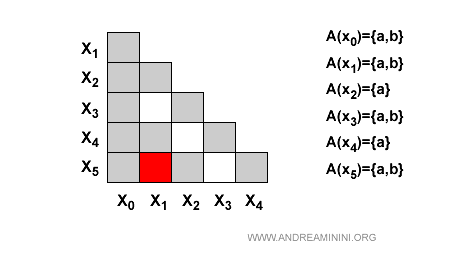
Coppia x2,x4
$$ \begin{cases} δ(x_2,a)=x_5 \\ δ(x_4,a)=x_5 \end{cases} $$
La casella {x5,x5} non è marcata. E' un confronto diretto.
$$ \begin{cases} δ(x_2,b)={} \\ δ(x_4,b)={} \end{cases} $$
La casella non esiste.
Coppia x3,x5
$$ \begin{cases} δ(x_3,a)=x_4 \\ δ(x_5,a)=x_2 \end{cases} $$
La casella {x4,x5}={x4,x5} è già marcata.
Quindi, non serve controllare anche l'evento b.
La coppia confrontata {x3,x5} va eliminata dalla tabella.
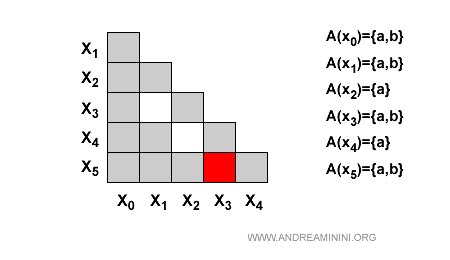
Le coppie (bianche) rimanenti nella tabella sono gli stati indistinguibili dell'automa.
Pertanto, sono indistinguibili tra loro gli stati
$$ x_1 ≈ x_3 \\ x_2 ≈ x_4 $$
Una volta trovati gli stati indistinguibili posso eliminarli.
Tra gli stati x1≈x3 scelgo come rappresentativo x1.
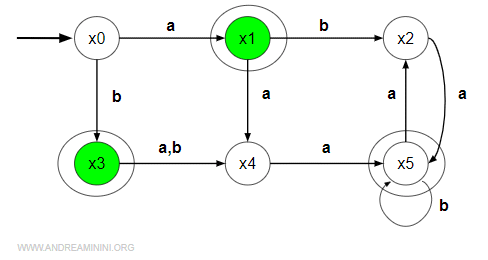
Sposto le transizioni in entrata da x3 a x1.
Elimino le transizioni in uscita da x3 ed elimino lo stato x3.
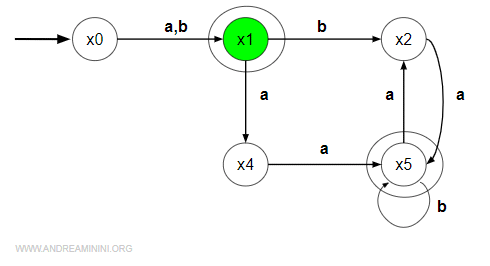
Tra gli stati x2≈x4 scelgo come rappresentativo x2.
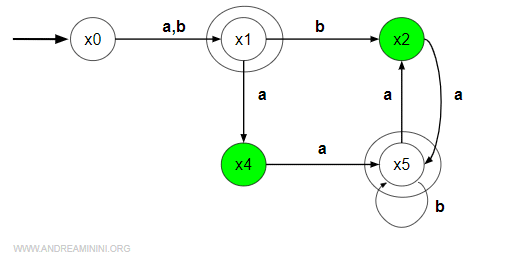
Sposto le transizioni in entrata da x4 a x2.
Elimino le transizioni in uscita da x4 ed elimino lo stato x2.
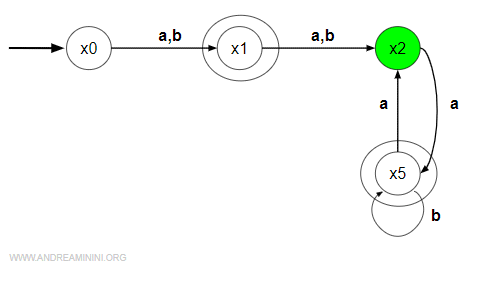
Ho ottenuto l'automa minimo.
E' equivalente all'automa iniziale, ha lo stesso linguaggio accettato ma un numero di stati inferiore.
E così via.
