Come trasformare un automa non deterministico AFN in AFD
Qualsiasi automa a stati finiti non deterministico (AFN o NFA) può essere trasformato in automa determinstico (AFD o DFA).
Un esempio pratico
Ho il seguente automa non deterministico (NFA) su un insieme di simboli E={a,b} e 5 stati.
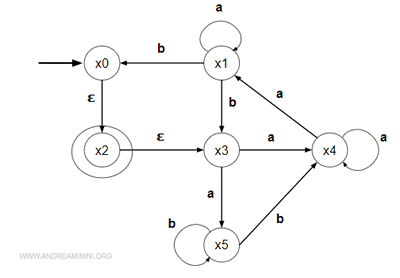
Per ciascun stato associo gli stati raggiungibili sia per le e-transizioni che per le ε-transizioni.
| ε | a | b | |
|---|---|---|---|
| x0 | x0,x2,x3 | Ø | Ø |
| x1 | x1 | x1 | x0,x3 |
| x2 | x2,x3 | Ø | Ø |
| x3 | x3 | x4,x5 | Ø |
| x4 | x4 | x1,x4 | Ø |
| x5 | x5 | Ø | x4,x5 |
Nota. Ogni stato (nodo) ha sempre una transizione vuota (ε) con se stesso anche se non è indicata nel grafo.
A questo punto credo due insiemi di stati
- X' è l'insieme degli stati del nuovo automa deterministico AFD
- X'N è l'insieme degli stati del vecchio automa non deterministico AFN da analizzare
Inizialmente X' è vuoto
$$ X'=\{ \} $$
Definisco il nodo iniziale x'0 del nuovo automa AFD e gli assegno i nodi raggiungibili da x0.
$$ x'_0 = \{ x_0,x_2,x_3 \} $$
Nota. In questo modo comincio a costruire l'automa AFD equivalente.

Poi aggiungo x'0 ai nodi da esplorare
$$ X'_N=\{ x'_0 \} $$
Analisi nodo x'0
Estraggo x'0 da X'N e trovo gli stati raggingibili.
- A(x'0,e) contiene le transizioni da x'0 agli altri stati per ciascun simbolo (a,b)
- B(x'0,e) contiene le transizioni da A(x'0,e) con zero o più ε-transizioni vuote
Quindi
$$ A(x'_0,a) = A(\{ x_0,x_2,x_3 \},a) = \{ x_4,x_5 \}$$
In pratica seleziono tutti gli stati raggiungibili con 'a' dall'insieme di stati x0,x2,x3 del vecchio automa AFN
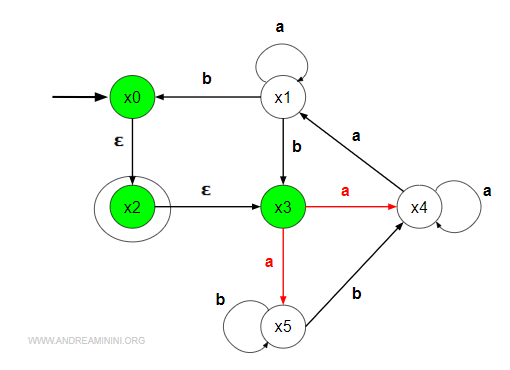
Poi verifico tra gli stati raggiunti {x4,x5} tramite il simbolo 'a' quali sono le ∈-transizioni.
$$ B(x'_0,a) = B(\{ x_4,x_5 \},a) = \{ x_4,x_5 \}$$
Gli stati {x4,x5} non hanno ε-transizioni a parte con se stessi.
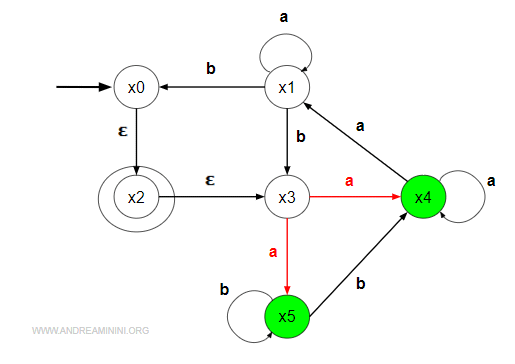
Verifico se esiste una transizione B nell'insieme degli stati del nuovo automa AFD
$$ X' = \{ x'_0 \} $$
Non esiste, quindi aggiungo sul nuovo automa un nuovo stato x'1 uguale a B.
$$ x'_1 = B(x'_0,a) = \{ x_4,x_5 \} $$
e una nuova transizione ∂ da x'0 a x'1 per il simbolo 'a'
$$ ∂(x'_0,a)=x'_1 $$
Nota. Sul grafo del nuovo automa AFD si aggiunge un nuovo stato e una nuova transizione.
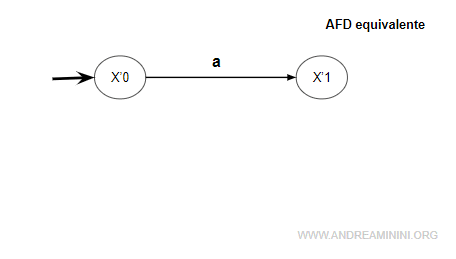
Ora gli insiemi degli stati è
$$ X' = \{ x'_0, x'_1 \} $$
Aggiungo il nuovo nodo anche nell'insieme dei nodi da esplorare
$$ X'_N \{ x'_0, x'_1 \} $$
A questo punto ripeto la stessa procedura per analizzare x'0 per l'evento 'b'.
$$ A(x'_0,b) = A(\{ x_0,x_2,x_3 \},b) = \{ \}$$
Non ci sono nodi raggiungibili, quindi la transizione non è definita per 'b'.
Come ultimo passo elimino lo stato appena analizzato x'0 dall'insieme dei nodi da esplorare.
$$ X'_N \{ x'_1 \} $$
Analisi nodo x'1
Estraggo x'1 da X'N e trovo gli stati raggingibili.
$$ A(x'_1,a) = A(\{ x_4,x_5 \},a) = \{ x_1,x_4 \}$$
Sono gli unici stati raggiungibili tramite 'a' dagli stati di x'1 ossia da x4 e x5.

Poi verifico tra gli stati raggiunti {x1,x4} tramite il simbolo 'a' quali sono le ∈-transizioni.
$$ B(x'_1,a) = B(\{ x_1,x_4 \},a) = \{ x_1,x_4 \}$$
Gli stati {x1,x4} non hanno ε-transizioni a parte con se stessi.
Verifico se esiste una transizione B nell'insieme degli stati del nuovo automa AFD
$$ X' = \{ x'_0, x'_1 \} $$
Nota. Dove $$ x'_0 = \{ x_0,x_2,x_3 \} $$ $$ x'_1 = \{ x_4,x_5 \} $$
Non esiste, quindi creo e aggiungo un nuovo stato x'2.
$$ x'_2 = B(x'_1,a) = \{ x_1,x_4 \} $$
e una nuova transizione ∂ da x'1 a x'2 per il simbolo 'a'
$$ ∂(x'_1,a)=x'_2 $$
Nota. Sul grafo del nuovo automa AFD si aggiunge un nuovo stato e una nuova transizione.
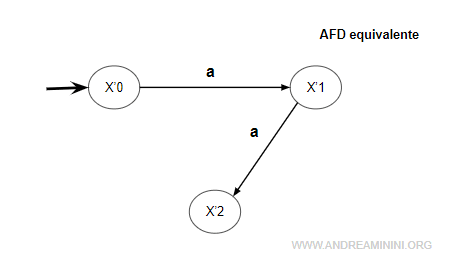
Ora gli insiemi degli stati è
$$ X' = \{ x'_0, x'_1, x'_2 \} $$
Aggiungo il nuovo nodo anche nell'insieme dei nodi da esplorare
$$ X'_N \{ x'_1, x'_2 \} $$
A questo punto ripeto la stessa procedura per analizzare x'1 per l'evento 'b'.
$$ A(x'_1,b) = A(\{ x_4,x_5 \},b) = \{ x_4,x_5 \}$$
Da x4 e x5 ci sono due e-transizioni tramite 'b' verso x4 e x5 (cappio).
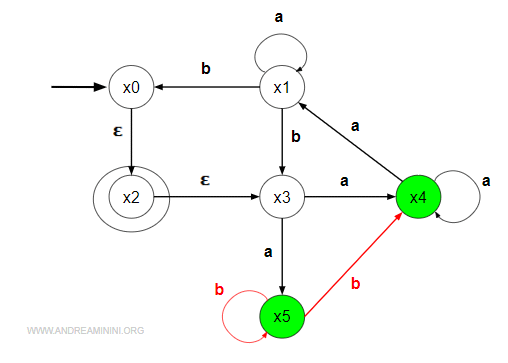
Poi verifico tra gli stati raggiunti {x1,x4} tramite il simbolo 'b' quali sono le ∈-transizioni.
$$ B(x'_1,b) = B(\{ x_4,x_5 \},b) = \{ x_4,x_5 \}$$
Gli stati {x4,x5} non hanno ε-transizioni a parte con se stessi.
Verifico se esiste una transizione B={x4,x5} nell'insieme degli stati del nuovo automa AFD
$$ X' = \{ x'_0, x'_1, x'_2 \} $$
Nota. Dove $$ x'_0 = \{ x_0,x_2,x_3 \} $$ $$ x'_1 = \{ x_4,x_5 \} $$ $$ x'_2 = \{ x_1,x_4 \} $$
La transizione B={x4,x5} esiste già. E' lo stato x'1.
Quindi non creo un nuovo stato e aggiungo soltanto una e-transizione ∂ da x'1 a x'1 per il simbolo 'a'
$$ ∂(x'_1,b)=x'_1 $$
Nota. Sul grafo del nuovo automa AFD si aggiunge una nuova transizione.
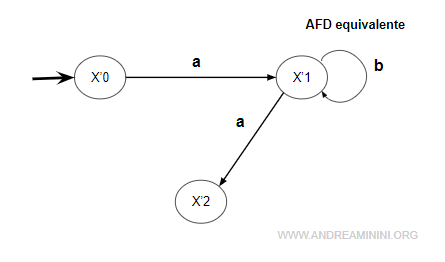
Come ultimo passo elimino lo stato appena analizzato x'1 dall'insieme dei nodi da esplorare.
$$ X'_N \{ x'_2 \} $$
Analisi nodo x'2
Estraggo x'1 da X'N e trovo gli stati raggingibili tramite il simbolo 'a'.
$$ A(x'_2,a) = A(\{ x_1,x_4 \},a) = \{ x_1,x_4 \}$$
Sono gli stati raggiungibili tramite 'a' da x'2 ossia da x1 e x4 dell'automa AFN.
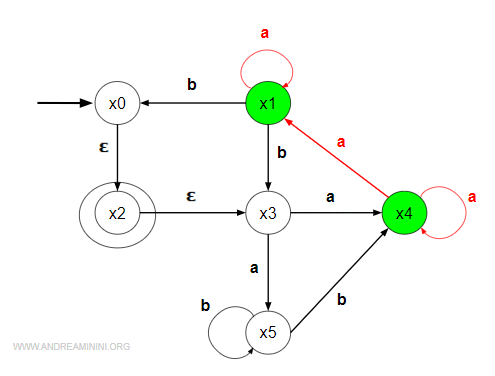
Poi verifico tra gli stati raggiunti {x1,x4} tramite il simbolo 'a' quali sono le ∈-transizioni.
$$ B(x'_2,a) = B(\{ x_1,x_4 \},a) = \{ x_1,x_4 \}$$
Gli stati {x1,x4} non hanno ε-transizioni a parte con se stessi.
Verifico se esiste una transizione B={x1,x4} nell'insieme degli stati del nuovo automa AFD
$$ X' = \{ x'_0, x'_1, x'_2 \} $$
Nota. Dove $$ x'_0 = \{ x_0,x_2,x_3 \} $$ $$ x'_1 = \{ x_4,x_5 \} $$ $$ x'_2 = \{ x_1,x_4 \} $$
Esiste già, è la transizione x'2.
Quindi aggiungo una transizione ∂ da x'2 a x'2 per il simbolo 'a' ossia un cappio.
$$ ∂(x'_2,a)=x'_2 $$
Nota. Sul grafo del nuovo automa AFD si aggiunge una nuova transizione.
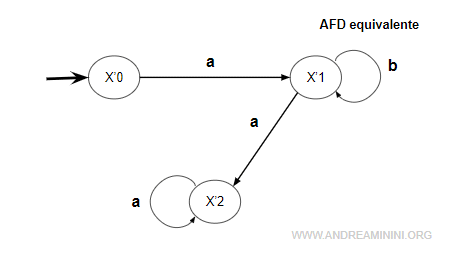
Infine ripeto la stessa procedura per analizzare x'2 per l'evento 'b'.
$$ A(x'_2,b) = A(\{ x_1,x_4 \},b) = \{ x_0,x_3 \}$$
Gli stati x0,x3 sono raggiungibili da x'2={x1,x4} tramite il simbolo 'b'.
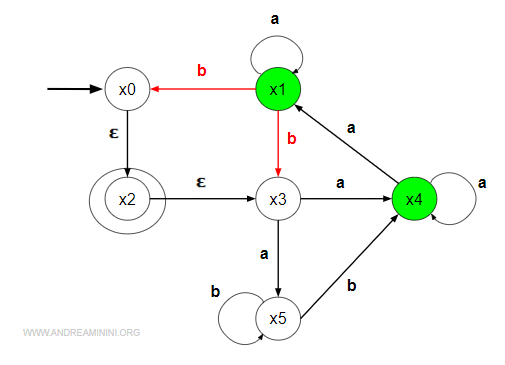
Verifico tra gli stati raggiunti {x0,x3} tramite il simbolo 'b' quali sono le ∈-transizioni.
$$ B(x'_2,b) = \{ x_0,x_2,_3 \}$$
Gli stati {x0,x3} hanno una ε-transizioni con se stessi.
Inoltre, lo stato x0 ha una ε-transizioni verso x2.
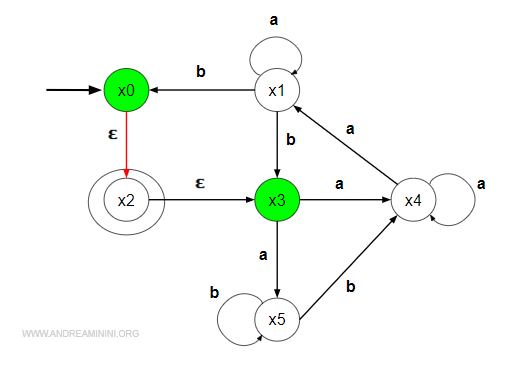
Verifico se esiste una transizione B={x0,x2,x3} nell'insieme degli stati del nuovo automa AFD
$$ X' = \{ x'_0, x'_1, x'_2 \} $$
Nota. Dove $$ x'_0 = \{ x_0,x_2,x_3 \} $$ $$ x'_1 = \{ x_4,x_5 \} $$ $$ x'_2 = \{ x_1,x_4 \} $$
Esiste già. E' lo stato x'0.
Quindi aggiungo una nuova transizione ∂ da x'2 a x'0 per il simbolo 'b'
$$ ∂(x'_2,b)=x'_0 $$
Nota. Sul grafo del nuovo automa AFD si aggiunge un nuovo stato e una nuova transizione.
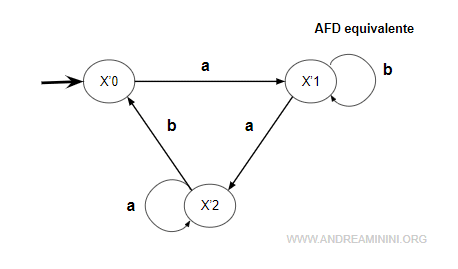
Come ultimo passo elimino lo stato appena analizzato x'2 dall'insieme dei nodi da esplorare.
$$ X'_N \{ \} $$
L'insieme degli stati da esplorare è vuoto.
L'algoritmo termina qui.
Gli stati finali dell'automa
Una volta costruito l'automa AFD equivalente bisogna individuare gli stati finali.
Nell'automa AFN originario lo stato terminale era lo stato x2.

L'automa AFD appena costruito è composto dai seguenti nodi:
$$ x'_0 = \{ x_0,x_2,x_3 \} $$ $$ x'_1 = \{ x_4,x_5 \} $$ $$ x'_2 = \{ x_1,x_4 \} $$
Seleziono come stati finali dell'automa AFD quelli che contengono lo stato finale dell'AFN (x2).
Soltanto lo stato x'0 contiene x2.
Pertanto, posso marcare x'0 come stato finale dell'automa AFD equivalente.
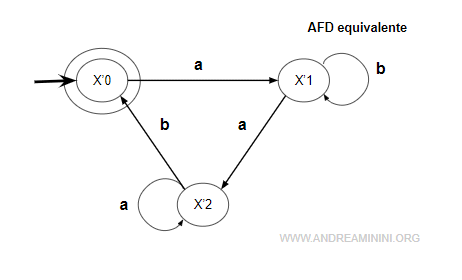
Ho così costruito l'automa deterministico AFD equivalente all'automa non deterministico AFN.
E così via.
