Le catene di Markov a tempo continuo
Una catena di Markov a tempo continuo è caratterizzata da transizioni di stato che avvengono in qualsiasi istante di tempo t. E' una tripla $$ \{ X, Q(t), π(0) \}$$
dove
- X è l'insieme degli stati della catena
- Q(t) è la matrice dei tassi di transizione all'istante t
- π(0) è il vettore della probabilità di stato iniziale
Come funziona
La probabilità di spostarsi dallo stato xi nell'istante t1 allo stato xj nell'istante t2 è definita nella funzione di transizione.
$$ p_{ij}(t_1,t_2) = Pr\{x(t_2)=x_j|x(t_1)=x_i \} $$
La probabilità di transitare dallo stato xi in un qualsiasi altro stato dall'istante t1 all'istante t2 è uguale a 1.
$$ \sum_{ x_j \in X } p_{ij}(t_1,t_2)=1 $$
Tutte le probabilità di transizione dall'istante t1 all'istante t2 sono inserite nella matrice delle probabilità di transizione.
$$ P(t_1,t_2) = [ p_{ij}(t_1,t_2) ] $$
Al variare di t1 e t2 esistono infinite matrici di transizione.
In ogni istante temporale (t) esiste un vettore delle probabilità di stato che indica la probabilità dell'automa di trovarsi in un particolare stato xj nell'istante t.
$$ π(t) = [π_0(t), π_1(t), ... ] $$
L'equazione di evoluzione dinamica agli stati successivi è
$$ π(t+Δt) = π(t)P(t,t+Δt) $$
Quindi, la probabilità di trovarsi in uno stato j nell'istante succesivo è
$$ π_j(t+Δt) = \sum_{x_i \in X} p_{ij} (t,t+Δt) \cdot π_j(t) $$
La catena di Markov omogenea
La catena di Markov a tempo continuo è detta omogenea se le probabilità di transizione non dipendono dai singoli istanti di tempo ma dalla loro differenza ξ=t2-t1. $$ p_{ij} (t_1, t_1+ξ) = p_{ij}(ξ) = Pr \{ x(t_1+ξ)=x_j|x(t_1)=x_i \} $$
Una catena omogenea è anche detta tempoinvariante.
Una matrice delle probabilità di transizione omogenea si indica con il simbolo
$$ P(ξ) $$
L'equazione di Chapman-Kolmogorov
Una volta fissato un istante intermedio ζ∈[t1,t2] ( ossia t1<ζ<t2 ) e posso costruire l'equazione di Chapman-Kolmogorov
$$ p_{ij}(t_1,t_2) = \sum_{x_r \in X} p_{ir}(t_1,ζ) \cdot p_{rj}(ζ,t_2) $$
che in forma matriciale è
$$ P(t_1,t_2) = P(t_1,ζ) \cdot P(ζ,t_2) $$
se t è un valore intermedio qualsiasi t1<t<t2
allora t2=t+Δt diventa
$$ P(t_1,t+Δt) = P(t_1,t) \cdot P(t,t+Δt) $$
Sottraggo a entrambi i membri P(t1,t)
$$ P(t_1,t+Δt) - P(t_1,t) = P(t_1,t) \cdot P(t,t+Δt) - P(t_1,t) $$
$$ P(t_1,t+Δt) - P(t_1,t) = P(t_1,t) \cdot ( P(t,t+Δt) -1 ) $$
Poi calcolo il limite per Δt che tende a zero.
$$ \lim_{Δt \rightarrow 0} \frac{P(t_1,t+Δt) - P(t_1,t)}{Δt} = \lim_{Δt \rightarrow 0} \frac{P(t_1,t) \cdot ( P(t,t+Δt) -1 )}{Δt} $$
Il primo membro è la derivata di P(t1,t) rispetto a t.
$$ P'(t_1,t) = \lim_{Δt \rightarrow 0} \frac{P(t_1,t) \cdot ( P(t,t+Δt) -1 )}{Δt} $$
Ora modifico il secondo membro
$$ P'(t_1,t) = P(t_1,t) \cdot \lim_{Δt \rightarrow 0} \frac{ ( P(t,t+Δt) -1 )}{Δt} $$
Il secondo limite è detto matrice dei tassi di transizione ( o generatore infinitesimale ).
$$ Q(t) = \lim_{Δt \rightarrow 0} \frac{ ( P(t,t+Δt) -1 )}{Δt} $$
In questo modo ottengo l'equazione differenziale di Chapman-Kolmogorov in avanti (forward).
$$ P'(t_1,t) = P(t_1,t) \cdot Q(t) $$
Nota. L'equazione differenziale di Chapman-Kolmogorov in indietro (backward) è la seguente: $$ P'(t_1,t) = -Q(t) \cdot P(t_1,t) $$
che in caso di tempoinvarianza diventa
$$ P'(ξ) = P(ξ) \cdot Q $$
Nota. In questo caso la matrice Q non dipende più dal tempo. Per questo si scrive Q e non Q(t). Se la probabilità iniziale è 1 su uno stato (stato iniziale) la soluzione dell'ultima equazione è $$ P(ξ) = e^{Qξ} $$ per ogni ξ ∈ R ed eQξ è uguale a $$ e^{Qξ} = \sum_h \frac{(Qξ)^h}{h!} $$
Inoltre, se la matrice è omogenea, la derivata dell'equazione di evoluzione dinamica della catena diventa
$$ π'(t) = π(t)Q(t) = π(t)Q $$
La rappresentazione grafica
Una catena di Markov a tempo continuo si rappresenta con il diagramma delle transizioni di stato
Il diagramma delle transizioni di stato di una catena di Markov a tempo continuo è un grafo orientato dove ogni nodo è uno stato e ogni arco e pesato con la probabilità di transizione tra i nodi adiacenti in base al verso dell'arco.
Un esempio pratico
Ho la seguente catena a tre stati che rappresenta una coda a due sportelli.
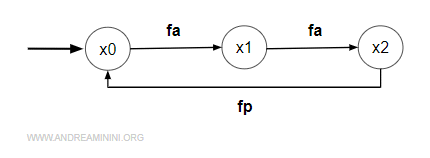
Gli eventi sono due: arrivo (a) e partenza (p).
Gli eventi di arrivo si presentano con frequenza fa mentre quelli di partenza con frequenza fp.
La matrice dei tassi di transizione Q è la seguente:
$$ Q = \begin{pmatrix} -fa & fa & 0 \\ 0 & - fa & fa \\ fp & 0 & -fp \end{pmatrix} $$
Prendendo i valori in colonna ottengo le equazioni differenziali delle probabilità di stato.
$$ π'_0(t) = -fa \cdot π_0(t) + fp \cdot π_2(t) $$
$$ π'_1(t) = fa \cdot π_0(t) - fa \cdot π_1(t) $$
$$ π'_2(t) = fa \cdot π_1(t) - fp \cdot π_2(t) $$
E così via.
