La catena di Markov a tempo discreto
La catena di Markov a tempo discreto è caratterizzata da uno spazio degli stati discreti e da un'evoluzione a tempo discreto. E' una tripla $$ (X, P(k), π(0)) $$
- X è lo spazio degli stati.
- P(k) è la matrice delle probabilità di transizione
- π(0) è la distribuzione delle probabilità iniziale
La matrice delle probabilità di transizione
La matrice delle probabilità di transizione P(k) è una matrice stocastica composta dalle probabilità di transizione a un passo da ogni stato x∈X agli altri nell'istante k.
$$ \begin{array}{c|lcr} & x'_0 & ... & x'_j \\ \hline x_0 & ... & ... & ... \\ \vdots & ... & ...& ... \\ x_i & ... & ...& p_{i,j} \end{array} \Rightarrow P= \begin{pmatrix} p_{0,0} & ... & p_{0,j} \\ \vdots & & \\ p_{i,0} & ... & p_{i,j} \end{pmatrix} $$
In ogni riga indico lo stato di partenza x(k) e in ogni colonna lo stato di destinazione x'(k+1) a un passo.
Nelle celle inserisco la probabilità di passare dallo stato x(k) allo stato x'(k+1).
$$ p_{i,j} = P(x(k+1)|x_(k)) = P(x_j|x_i) $$
La somma delle probabilità di ogni riga è uguale a 1 perché è la distribuzione della probabilità degli eventi di transizione a partire dallo stato x(k).
$$ \sum_{j} p_{i,j} (k) = 1 $$
La prima riga π(0) della matrice è la distribuzione della probabilità assoluta iniziale.
$$ π(0) = \{ x_j \} $$
Nota. Essendo una matrice stocastica gli elementi della matrice delle probabilità di transizione hanno tutti un valore compreso tra 0 e 1. La diagonale della matrice è formata dagli autovalori e almeno un autovalore è uguale a 1.
La probabilità assoluta di trovarsi in uno stato xi nell'istante k è
$$ π(k) = \{ π_0, π_1, ... , π_i \} $$
Ad esempio, la probabilità che l'automi si trovi nello stato x1 nell'istante k è π1.
Quindi la probabilità di trovarsi nello stato xj nell'istante k è
$$ π_j(k+1) = \sum_{i} p_{i,j} ·π_i(k) $$
Ovvero, la probabilità assoluta di trovarsi in uno degli stati x è
$$ π(k+1) = π(k) \cdot P $$
Mentre la probabilità di trovarsi in uno stato x dopo k passi è determinata dall'equazione di evoluzione
$$ π(k) = π(0) \cdot P(0) \cdot P(1) \cdot \cdot \cdot P(k-1) $$
Nota. Quest'ultima formula può essere ottimizzata usando altre equazioni di evoluzione più efficienti. Ad esempio, l'equazione di Chapman-Kolmogorov.
Tipi di matrici di transizione
Esistono due tipologie di matrici di transizione
- Omogenea
La matrice di transizione P è omogenea quando le probabilità delle transizioni di stato non dipendono dall'istante k. Le probabilità di transizione sono costanti. In pratica, la matrice è tempoinvariante. - Non omogenea
La matrice di transizione P è non omogenea quando le probabilità delle transizioni di stato dipendono dall'istante k. Le probabilità di transizione sono variabili.
Un esempio pratico
Lo spazio degli stati dell'automa è composto da soli due stati dove x0 è lo stato iniziale.
$$ X = \{ x_0, x_1 \} $$
La probabilità della transizione da x0 a x1 è p(k).
$$ P_{x_0,x_1}(k) = P(x_1|x_0) = p(k) $$
Nota. Di conseguenza, la probabilità di restare nello stato x0 è $$ P_{x_0,x_0}(k) = P(x_0|x_0) = 1-p(k) $$
Viceversa, la probabilità della transizione da x1 a x0 è nulla.
$$ P_{x_1,x_0}(k) = P(x_0|x_1) = 0 $$
Nota. Di conseguenza, la probabilità di restare nello stato x1 è $$ P_{x_1,x_1}(k) = P(x_1|x_1) = 1 $$
Dal punto di vista grafico posso rappresentare la catena con un digrafo detto diagramma delle transizioni di stato.
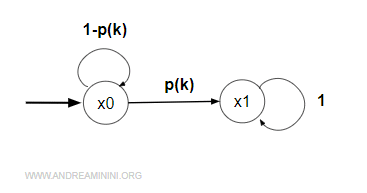
La matrice delle transizioni è la seguente
$$ \begin{array}{c|lcr} & x_0 & x_1 \\ \hline x_0 & 1-p(k) & p(k) \\ x_1 & 0 & 1 \end{array} $$
Dove nella riga è indicato lo stato iniziale x(k) e nelle colonne lo stato di destinazione x(k+1).
Nella forma matematica corretta la matrice è
$$ P = \begin{pmatrix} 1-p(k) & p(k) \\ 0 & 1 \end{pmatrix} $$
Nota. La diagonale della matrice è composta dagli autovalori. Gli autovalori sono minori di 1 e almeno un autovalore è uguale a 1.
Quindi, nell'istante k=0 iniziale l'automa si trova nello stato x0 perché è lo stato iniziale.
$$ π(0) = \{ 1, 0 \} $$
Nell'istante k=1 la probabilità di trovarsi nello stato x0 e x1 è uguale al prodotto tra le probabilità π(0) e la matrice delle transizioni P.
$$ π(1) = π(0) \cdot P $$
$$ π(1) = \{ 1, 0) \} \cdot \begin{pmatrix} 1-p(k) & p(k) \\ 0 & 1 \end{pmatrix} $$
$$ π(1) =\{ 1-p(k), p(k) \} $$
Nell'istante k=2 la probabilità di trovarsi nello stato x0 e x1 è uguale al prodotto tra le probabilità π(1) e la matrice delle transizioni P.
$$ π(2) = π(0) \cdot P $$
$$ π(2) = \{ 1-p(k), p(k) \} \cdot \begin{pmatrix} 1-p(k) & p(k) \\ 0 & 1 \end{pmatrix} $$
$$ π(2) = \{ (1-p(k))(1-p(k)) , (1-p(k) \cdot p(k) + p(k) \} $$
Spiegazione. La probabilità di essere nello stato x0 in k=2 è pari al prodotto (1-p(k))(1-p(k)). La probabilità di trovarsi in x1 in k=2 è la somma delle probabilità di due sequenze di transizioni possibili (x0,x1) e (x1,x1) ossia la prima (1-p(k))p(k) e la seconda p(k).
Esempio con i dati
Se la probabilità di transitare da x0 a x1 è 0.20.
$$ p(k)=0.20 $$
La matrice delle probabilità di transizione all'istante k=0 è
$$ P(0) = \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} $$
La prima riga della matrice indica la distribuzione della probabilità assoluta iniziale.
$$ π(0) = \{ 0.20 , 0.80 \} $$
La matrice delle probabilità di transizione all'istante k=1 è
$$ π(1) = π(0) \cdot P(0) $$
$$ π(1) = ( 0.20, 0.80 ) \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} $$
$$ π(1) = \{ 0.20 \cdot 0.20 + 0.80 \cdot 0 , 0.20 \cdot 0.80 + 0.80 \cdot 1 \} $$
$$ π(1) = \{ 0.04 , 0.96 \} $$
La matrice delle probabilità di transizione all'istante k=2 è
$$ π(2) = π(0) \cdot P(0) \cdot P(1) $$
$$ π(2) = ( 0.20, 0.80 ) \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0.20 & 0.80 \\ 0 & 1 \end{pmatrix} $$
$$ π(2) = ( 0.20, 0.80 ) \cdot \begin{pmatrix} 0.04 & 0.96 \\ 0 & 1 \end{pmatrix} $$
$$ π(2) = \{ 0.008 , 0.992 \} $$
E così via.
