Automi temporizzati deterministici
Un automa temporizzato deterministico considera gli eventi e il tempo in cui si verificano. E' deterministico perché l'automa conosce l'istante temporale in cui si verificano gli eventi.
Un automa temporizzato deterministico G è caratterizzato da una 5-upla
$$ G=(X,x_0,Σ, δ,θ) $$
Dove i parametri hanno questo significato
- X è l'insieme degli stati possibili dell'automa ( spazio degli stati )
- x0 è lo stato iniziale dell'automa
- Σ è l'insieme degli eventi ammissibili
- δ è la funzione di transizione da uno stato all'altro
- θ è la struttura di temporizzazione deterministica
Come funziona
L'automa temporizzato deterministico passa da uno stato a un altro tramite la funzione di transizione come qualsiasi DFA
$$ x' = δ(x, e) $$
L'evento (e) è determinato dall'orologio dell'evento oe
La variabile oe indica fra quanto tempo si verifica il prossimo evento e.
Nota. La variabile oe è sempre aggiornata rispetto al momento corrente perché è l'intervallo di tempo tra l'istante corrente t e l'istante t' in cui si verificherà il successivo evento ossia (t'-t).
La struttura di temporizzazione deterministica è l'insieme θ delle sequenze dei ritardi di attivazione per ogni evento e ∈ Σ.
$$ θ=\{ θ_{e,1}, θ_{e,2}, ...\} $$
Dove ogni elemento è il k-esimo ritardo dell'evento e ∈ Σ.
Il ritardo di attivazione è il lasso di tempo tra l'attivazione e il verificarsi dell'evento.
Può essere una sequenza oppure un valore costante.
- Esempio (sequenza). L'evento k=2 ha la seguente struttura di temporizzazione $$ θ_2 = \{ 1,3,2,5,... \} $$ La prima volta che si verifica l'evento k=2 ha un ritardo di attivazione pari a 1, la seconda volta pari a 3, la terza pari a 2 e così via.
- Esempio (valore costante). Se la sequenza è composta soltanto da un valore, il ritardo di attivazione dell'evento è costante. $$ θ_2 = \{ 1 \:\: \forall k \in N \} $$ In questo caso il ritardo di attivazione dell'evento e2 è sempre pari a 1.
L'indice k è detto contatore di attivazione e indica il numero di volte che l'evento è stato attivato dall'istante iniziale.
Nell'istante iniziale sono posti di default a ke=1 tutti gli eventi ammissibili dallo stato x0 ossia e∈(x0).
L'automa calcola gli orologi degli eventi ossia il tempo minimo degli eventi successivi a partire dall'istante attuale, tenendo conto anche dei ritardi di attivazione.
Poi sceglie l'evento più vicino nel tempo come evento successivo.
Un esempio pratico
Questo automa temporizzato gestisce il flusso in una coda dove i clienti possono entrare (in), spostarsi di stato o uscire (out).
Lo spazio degli eventi è composto da due eventi in (i) e out (o)
$$ Σ=\{ i, o \} $$
Lo spazio degli stati è un insieme infinito numerabile con i numeri naturali
$$ X=\{ 0,1,2,3,... \} $$
Gli eventi attivi per ogni stato sono {i,o} ad eccezione dello stato 0 in cui è ammesso soltanto l'evento {i}
$$ \begin{cases} A(0)=\{i \} \\ A(x)=\{i,o\} \:\: \forall x>0 \end{cases} $$
L'equazione degli stati di una coda è molto semplice.
$$ δ(e,X) = \begin{cases} x+1 \:\:\: se \:\: e=i \\ x-1 \:\:\: se \:\: e=o \: ∧ \: x>0 \end{cases} $$
La struttura di temporizzazione è
$$ θ=\{ θ_{i}, θ_{o}, ...\} $$
dove i ritardi di attivazione sono delle sequenze di interi
$$ θ_{i} = \{ 1,2,2,2, ...\} \\ θ_{o} = \{ 4,2,2,2, ...\} $$
Una volta nota la struttura di temporizzazione l'automa può prevedere la sequenza degli eventi.
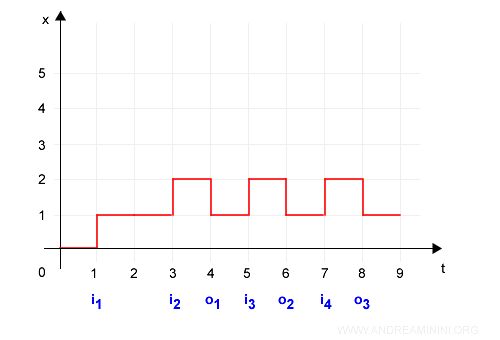
Nota. Il primo ingresso si verifica con un ritardo pari a 1 poiché θi={1,2,2,...}. La prima uscita con un ritardo pari a 4 in quanto θo={4,2,2,...}. Queste informazioni sono già note perché indicate nella struttura di temporizzazione. Il ritardo θ si calcola dall'ultimo evento accaduto dello stesso tipo. Ad esempio, il secondo ingresso i2 si verifica all'istante 3 poiché θi={1,2,2,...} e l'ultimo evento i1 si è verificato nell'istante 1.
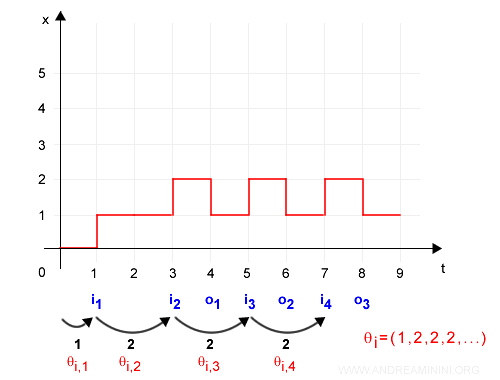
Allo stesso modo si spiegano i ritardi degli eventi in uscita. E via dicendo.
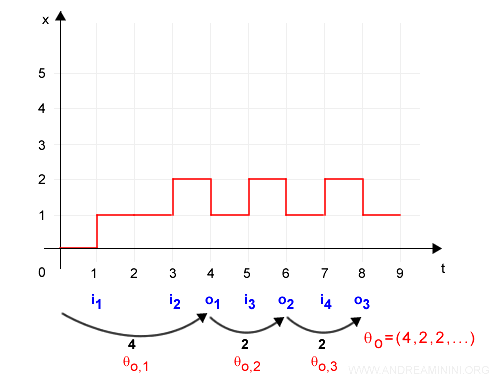
Nell'istante iniziale t=0 l'automa si trova nello stato x=0 ossia x0.
Gli orologi indicano il tempo per raggiungere l'evento successivo.
$$ o_i = 1 \\ o_o = nd $$
Nota. In questo stato è attivo soltanto l'evento di ingresso "i" ossia A(0)={i}. Per questa ragione l'orologio oo non è definito (nd).
L'automa calcola il valore minimo degli orologi o* ( tempo di intervento ).
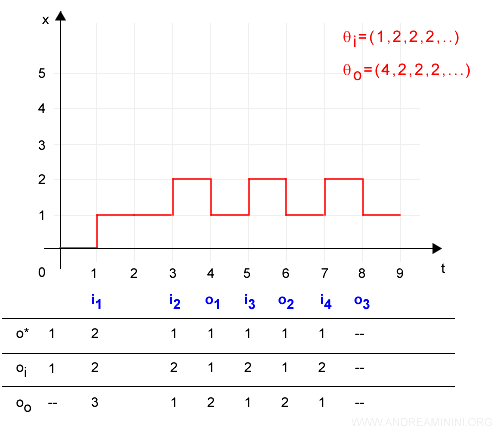
L'evento successivo (e') è determinato dall'evento con l'orologio minore.
$$ \begin{cases} e'=o \:\: se \:\: o_o<o_i \\ e'=i \:\: altrimenti \end{cases} $$
Se il tempo prima che si verifichi il prossimo evento out (oo) è inferiore al tempo dell'evento in (oi), allora l'evento successivo è l'uscita (out).
In caso contrario, l'evento successivo è l'entrata (in).
Nota. Inizialmente l'automa si trova nello stato x0. Essendo la coda vuota, il solo evento ammesso è l'ingresso A(0)={i}. Quindi, nel momento iniziale l'evento successivo e' è sicuramente un arrivo (input).
In questo caso è l'evento "i" perché oi=1 mentre oo=nd.
Una volta conosciuto l'evento successivo (e'), l'automa calcola lo stato successivo (x') tramite la funzione di transizione ( equazione di stato ).
$$ x' = δ(i,x_0) = x+1 = 0+1=1 $$
Poi calcola il tempo di accadimento (t') dell'evento successivo
In questo caso t'=1.
$$ t' = t + o* = 0 + 1 = 1 $$
Dopo aver individuato l'evento successivo (e') in base agli orologi oi e oo, l'automa aggiorna gli orologi dell'evento successivo o'i e o'o.
Gli orologi o' indicano quanto tempo deve passare perché si verifichi il successivo evento a partire dall'istante corrente.
$$ o'_e = \begin{cases} o_e - o* \:\:\: se \:\: e \ne e' \:∧ \: e \in A(x) \\ θ_{e,v_e+1} \end{cases} $$
In questo caso aggiorna soltanto o'i.
Poiché vi = 1.
$$ o'_i = θ_{i,v_i+1} = θ_{i,1+1} θ_{i,v_2} = 2 $$
Poi l'automa aggiorna anche i contatori di attivazione
$$ v'_e = \begin{cases} v_e +1 \:\:\: se \:\: e = e' \: \\ v_e \end{cases} $$
Nell'istante t=0 l'evento (e) è ancora nullo. Quindi vi resta uguale a 1.
In questa tabella elenco la sequenza degli eventi con l'istante in cui si verifica l'evento (t), l'evento successivo (e'), gli orologi (o) e i contatori (k).
| t | e | oi | oo | e' | oi' | oo' | ki | ko |
|---|---|---|---|---|---|---|---|---|
| 0 | -- | -- | -- | i1 | 1 | -- | 1 | --- |
| 1 | i1 | 1 | -- | i2 | 2 | 3 | 2 | --- |
| 3 | i2 | 2 | 3 | o1 | 1 | 2 | 2 | 1 |
| 4 | o1 | 1 | 2 | i3 | 2 | 1 | 3 | 1 |
| 5 | i3 | 2 | 1 | o2 | 1 | 2 | 3 | 2 |
| 6 | o2 | 1 | 2 | i4 | 2 | 1 | 4 | 2 |
| 7 | i4 | 2 | 1 | o3 | --- | --- | 4 | 3 |
| 8 | o3 | --- | --- | --- | --- | --- | 4 | 3 |
E così via.
