Automa minimo
Per ogni automa esiste un automa minimo che ha lo stesso linguaggio generato e accettato Lm ma un numero di stati inferiore.
L'automa è minimo è unico a parte gli isomorfismi ( diversa disposizione degli stati ).
A cosa serve un automa minimo?
Se un automa G raggiunge un determinato obiettivo con n stati, l'automa G' minimo fa lo stesso ma con m<n stati.
E' quindi più efficiente nell'utilizzo delle risorse e più semplice a parità di risultato.
Nota. Un automa minimo non necessariamente deve essere completo. Ciò che conta è che riduca al minimo il numero di stati a parità di comportamento dell'automa.
Un esempio pratico
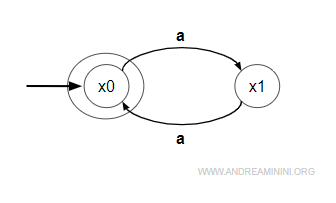
Questi due automi G,G' hanno lo stesso linguaggio generato L(G)=L(G') e accettato Lm(G)=Lm(G').
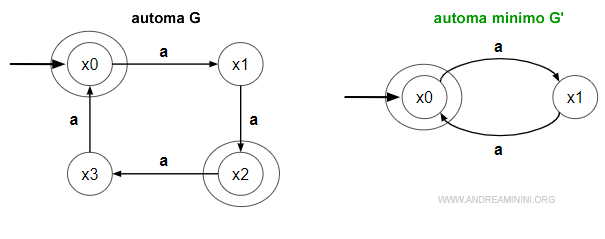
Il linguaggio accettato dai due automi è lo stesso
$$ L_m(G) = \{ a^n \} \\ L_m(G') = \{ a^n \} $$
Anche il linguaggio generato è lo stesso
$$ L(G) = \{ a^n \} \\ L(G') = \{ a^n \} $$
Quindi, il comportamento degli automi è identico ma il secondo ha un minore numero di stati.
E' più efficiente perché utilizza meno risorse.
Come minimizzare un automa deterministico
Per rendere minimo un automa DFA si cercano gli stati indistinguibili e si sostituiscono con un solo stato rappresentativo per tutti.
Cos'è uno stato indistinguibile?
Due stati x e x' sono indistinguibili se sono raggiungibili con la stessa parola w.
$$ L(G|x) = L(G|x') \\ L_m(G|x) = L_m(G|x') $$
Gli stati indistinguibili sono una classe di equivalenza [x].
Come trovare gli stati indistinguibili? Individuare gli stati indistinguibili è facile se l'automa è semplice ma può diventare difficoltoso quando l'automa ha molti stati e transizioni. In questi casi è meglio usare l'algoritmo di Hopcroft. E' una procedura utile per trovare gli stati indistinguibili in un digrafo complesso. Una volta individuati gli stati indistinguibili posso rimuoverli con la seguente procedura di minimizzazione.
I passi per minimizzare un automa DFA
- Scelgo uno stato x' nella classe di equivalenza [x] per rappresentare tutti gli altri stati della classe [x]\{x'}
- Elimino le transizioni in uscita dalla classe di equivalenza [x]/{x'}
- Sposto le transizioni in entrata nella classe di equivalenza [x]/{x'} verso lo stato x'
- Rimuovo tutti gli stati nella classe di equivalenza [x]/{x'}. In questo modo resta soltanto lo stato x'
- Se tra gli stati rimossi nella classe [x]/{x'} c'è anche il stato iniziale, marco lo stato x' come nuovo stato iniziale.
Un esempio pratico
In questo automa
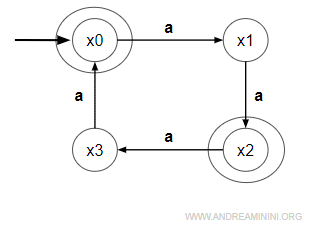
sono presenti due classi di equivalenza
$$ \{ a^n \: | \: n=pari \} = \{ x_0,x_2 \} $$
$$ \{ a^n \: | \: n=dispari \} = \{ x_1,x_3 \} $$
Nella prima classe scelgo x0 come rappresentativo di { x0,x2 }
Elimino le transizioni in uscita da x2 e rimando quelle in entrata da x2 verso x0. Poi elimino x2.
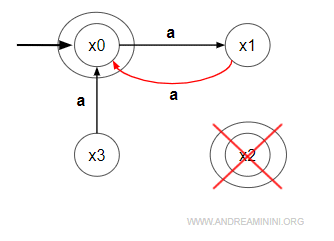
Nella seconda classe scelgo x1 come rappresentativo di { x1,x3 }
Elimino le transizioni in uscita da x3 e rimando quelle in entrata da x3 verso x1 (in questo caso non sono più). Poi elimino x3.
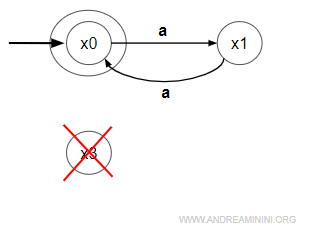
Il nuovo grafo mostra l'automa minimo.
E' composto da due stati e due transizioni.
E così via.
