Moltiplicazioni per un fattore da 11 a 19 con il metodo Trachtenberg
Il metodo Trachtenberg per le moltiplicazioni tra un numero qualsiasi e numeri compresi tra 11 e 19 prevede un sistema di calcolo semplificato che si svolge da destra verso sinistra.
La procedura si basa sulla moltiplicazione di una cifra del primo numero per l'ultima cifra del secondo numero, aggiungendo poi il numero precedente cioè la cifra immediatamente precedente nella sequenza.
Ecco i passaggi generali per eseguire la moltiplicazione:
- Scrivo i numeri con il numero a due cifre (ad esempio, 11, 12, ..., 19) come secondo fattore e l'altro numero come primo fattore.
- Moltiplico la cifra corrente del primo numero per l'unità del secondo numero
- Sommo la cifra precedente (se esiste) al risultato della moltiplicazione.
- Scrivo il risultato e prosegui con le altre cifre, procedendo da destra verso sinistra.
- Gestisco gli eventuali riporti sulla cifra successiva.
Un esempio pratico
Voglio calcolare la moltiplicazione tra i numeri
$$ 34 \times 13 $$
Prima iterazione
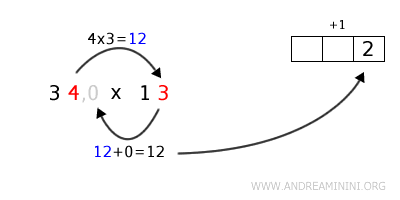
Moltiplico 4 per 3 (l'unità del secondo fattore) \( 4 \times 3 = 12 \).
Non aggiungo nulla al risultato perché non c'è una cifra precedente a 4 nel numero 34.
Quindi, scrivo 2 come ultima cifra del risultato e riporto 1
Secondo iterazione
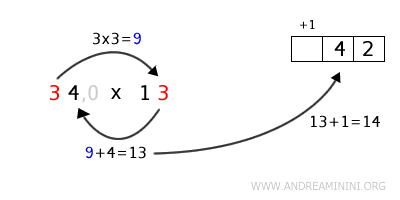
Passo alla cifra precedente di \( 34 \) che è 3.
Moltiplico 3 per 3 (l'unità del secondo fattore) \( 3 \times 3 = 9 \).
Aggiungo al risultato la cifra precedente che è 4 e ottengo \( 9 + 4 = 13 \)
Poiché c'è anche un riporto di 1, devo aggingerlo al risultato \( 13 + 1 = 14 \).
Quindi scrivo 4 nel risultato e riporto 1.
Terza iterazione
Infine, poiché non si sono altre cifre significativa da moltiplicare per l'unità del secondo fattore, aggiungo la prima cifra (3) al risultato.
Poiché devo considerare anche il riporto di 1 dell'iterazione precedente, scrivo \( 3 + 1 = 4 \).
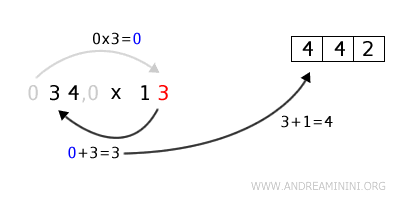
Il risultato finale è 442.
$$ 34 \times 13 = 442 $$
Riepilogando, il metodo di Trachtenberg per le moltiplicazioni con numeri tra 11 e 19 semplifica i calcoli utilizzando una procedura sistematica da destra verso sinistra, che sfrutta le somme parziali.
Questo approccio mi permette di ridurre i calcoli mentali necessari e velocizza il processo, una volta che ci si è abituati alla procedura.
Nota: in questo esempio ho scelto di moltiplicare \( 34 \times 13 \) per semplificare la spiegazione. Tuttavia, la stessa procedura si può applicare per moltiplicare per 11, 12, 13 e così via, fino a 19. Inoltre, il metodo può essere utilizzato con qualsiasi numero come primo fattore, anche molto grande. Ad esempio, $ 142137 \times 13 = 1847781 $
Il caso della moltiplicazione per 11
La moltiplicazione per 11 è ancora più semplice.
Poiché tutte le moltiplicazioni sono per 1, mi basta sommare ogni cifra del primo fattore con la cifra precedente.
Ad esempio, moltiplico 137 per 11
$$ 137 \times 11 = ???? $$
Scrivo la prima cifra (7) del numero 137 come unità del risultato.
$$ 137 \times 11 = ???7 $$
Sommo la seconda cifra (3) con la precedente cifra (7) del numero 137 e ottengo 3+7=10.
Quindi, scrivo 0 come seconda cifra del risultato e riporto di 1.
$$ 137 \times 11 = ??07 $$
Sommo la terza cifra (1) con la precedente cifra (3) del numero 137 e ottengo 1+3=4
In questo caso devo considerare anche il riporto dell'operazione precedente 4+1=5
Quindi scrivo 5 come terza cifra del risultato.
$$ 137 \times 11 = ?507 $$
Infine, non essendoci più altre cifre significative in 137 da sommare, scrivo la prima cifra (1) come quarta cifra del risultato.
$$ 137 \times 11 = 1507 $$
Il risultato della moltiplicazione è 1507.
E così via.
