La formula di MacLaurin della funzione coseno

Lo sviluppo della serie di MacLaurin della funzione coseno è $$ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - ... + \frac{(-1)^nx^{2n}}{(2n)!} + o(x^{2n}) $$

Dimostrazione

Considero la formula di MacLaurin

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$

In questo caso f(x)=cos(x)

Per k=0

Sapendo che la funzione f⁽⁰⁾=f(x)=cos(x)

$$ \frac{f^{(0)}(0)}{0!} \cdot x^0 = \frac{\cos(0)}{0!} \cdot x^0= \frac{1}{1} \cdot 1 = 1 $$

Quindi il primo termine della serie di MacLaurin è uno

$$ \cos(x) = 1 + o[x^0] $$

$$ \cos(x) = 1+o[1] $$

Per k=1

La derivata prima del coseno è -sin(x)

$$ \frac{f^{(1)}(0)}{1!} \cdot x^1 = \frac{D[\cos(0)]}{1!} \cdot x^1 = \frac{-\sin(0)}{1} \cdot x = \frac{0}{1} \cdot x = 0 $$

Quindi il secondo termine della serie di MacLaurin di ordine 1 è zero

$$ \cos(x) = 1 + 0 + o[x^1] $$

Per k=2

La derivata seconda del coseno è -cos(x)

$$ \frac{f^{(2)}(0)}{2!} \cdot x^2 = \frac{D^{(2)}\cos(0)}{2!} \cdot x^2 = \frac{-\cos(0)}{2!} \cdot x^2 = \frac{-1}{2} \cdot x^2 $$

Quindi il terzo termine della serie di MacLaurin di ordine 2 è

$$ \cos(x) = 1 + 0 - \frac{-1}{2} \cdot x^2 + o[x^2] $$

Per k=3

La derivata terza del coseno è sin(x)

$$ \frac{f^{(3)}(0)}{3!} \cdot x^3 = \frac{D^{(3)}\cos(0)}{3!} \cdot x^3 = \frac{\sin(0)}{3!} \cdot x^3 = \frac{0}{3!} \cdot x^3 = 0 $$

Quindi il quarto termine della serie di MacLaurin di ordine 3 è zero

$$ \cos(x) = 1 + 0 - \frac{1}{2} \cdot x^2 + 0 + o[x^3] $$

Per k=4

La derivata quarta del coseno è cos(x)

$$ \frac{f^{(4)}(0)}{4!} \cdot x^4 = \frac{D^{(4)}\cos(0)}{4!} \cdot x^4 = \frac{\cos(0)}{4!} \cdot x^4 = \frac{1}{4!} \cdot x^4 $$

Quindi il quinto termine della serie di MacLaurin di ordine 4 è

$$ \cos(x) = 1 + 0 - \frac{1}{2} \cdot x^2 + 0 + \frac{1}{4!} \cdot x^4 + o[x^4] $$

Per k=5

La derivata quinta del seno è -sin(x)

$$ \frac{f^{(5)}(0)}{5!} \cdot x^5 = \frac{D^{(5)}\cos(0)}{5!} \cdot x^5 = \frac{-\sin(0)}{5!} \cdot x^5 = \frac{0}{5!} \cdot x^5 = 0 $$

Quindi il sesto termine della serie di MacLaurin di ordine 5 è zero

$$ \cos(x) = 1 + 0 - \frac{1}{2} \cdot x^2 + 0 + \frac{1}{4!} \cdot x^4 + 0 + o[x^5] $$

In conclusione, la serie di MacLaurin di ordine 5 della funzione coseno è

$$ \cos(x) = 1 - \frac{1}{2} \cdot x^2 + \frac{1}{4!} \cdot x^4 + o[x^5] $$

Dal punto di vista grafico

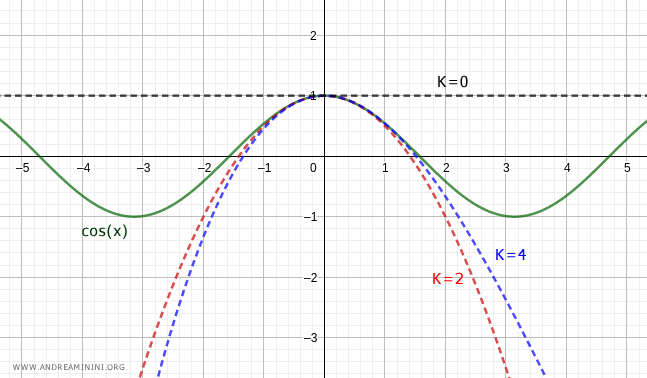
Nota. Come si può notare i termini della serie si alternano con valori nulli. Pertanto la serie di MacLaurin del coseno di ordine 4 $$ \cos(x) = 1 - \frac{1}{2} \cdot x^2 + \frac{1}{4!} \cdot x^4 + o[x^4] $$ e quella di ordine 5 $$ \cos(x) = 1 - \frac{1}{2} \cdot x^2 + \frac{1}{4!} \cdot x^4 + o[x^5] $$ sono praticamente uguali, salvo che per un "o piccolo" di ordine diverso alla fine.

E così via.