La mappa di Karnaugh
A cosa serve la mappa di Karnaugh
Le mappe di Karnaugh sono un metodo per semplificare un'espressione booleana o, è la stessa cosa, per ridurre il numero delle porte logiche in un circuito combinatorio.
Come trovare la mappa di Karnaugh
Il metodo funziona soltanto se l'espressione è in forma normale disgiuntiva ( DNF ).
$$ xyz + xy \overline{z} + \overline{x}y $$
Nota. Per ogni funzione logica esiste sempre un'espressione booleana in forma normale disgiuntiva ed è unica.
Inoltre, le clausole devono essere composte dagli stessi letterali.
Esempio
Questa espressione booleana è composta da tre clausole.
$$ xyz + xy \overline{z} + \overline{x}y $$
La terza clausola non ha il letterale z.
Per risolvere il problema, la trasformo in una somma di clausole con la z attiva e negata.
$$ xyz + xy \overline{z} + ( \overline{x}yz + \overline{x}y\overline{z} ) $$
$$ xyz + xy \overline{z} + \overline{x}yz + \overline{x}y\overline{z} $$
Nota. Questa espressione booleana equivale a un circuito logico con quattro porte AND, una porta OR e quattro porte NOT. Complessivamente, il circuito è composto da 9 porte.
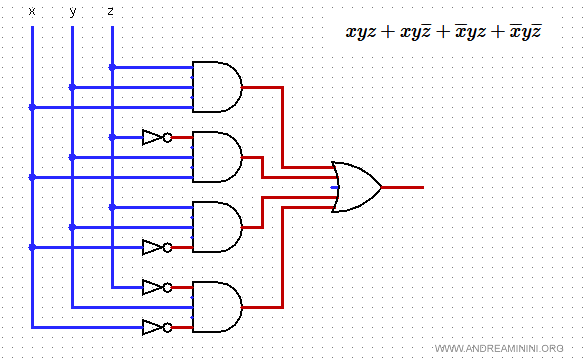
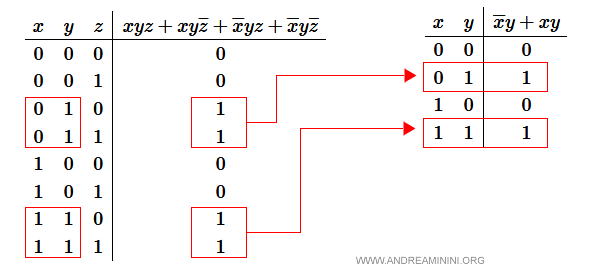
La tavola di verità dell'espressione è
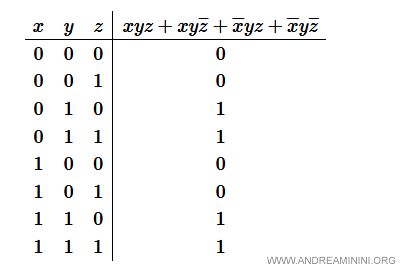
1] Costruire la mappa
Scelgo due gruppi di letterali dell'espressione. Ad esempio xy e z.
Poi costruisco una tabella mettendo le xy sulle colonne e la z sulle righe.
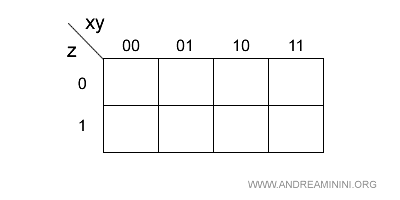
Nelle righe e nelle colonne indico le combinazioni di valori (0,1) che i letterali x e xy possono assumere.
2] Individuare le celle della mappa a cui corrispondono le clausole dell'espressione
A questo punto, verifico quali celle si collocano le clausole dell'espressione booleana.
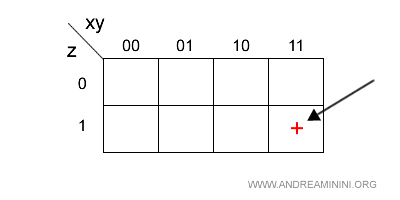
Prima clausola
La prima clausola dell'espressione è
$$ xyz $$
Equivale a xy=11 * z=1.
Questa clausola corrisponde alla cella in cui si incrociano l'ultima colonna (xy=11) e la seconda riga (z=1) della mappa.
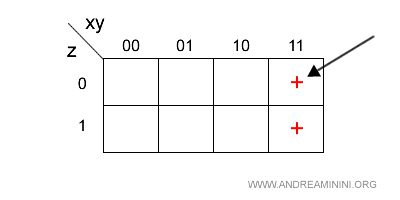
Seconda clausola
La seconda clausola dell'espressione è
$$ xy \overline{z} $$
Equivale a xy = 11 e z=0.
Questa clausola corrisponde alla cella in cui si incrociano l'ultima colonna (xy=11) e la prima riga (z=0) della mappa.
Terza clausola
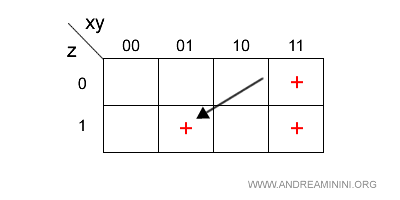
La terza clausola dell'espressione è
$$ \overline{x}yz $$
Equivale a xy = 01 e z=1.
Questa clausola corrisponde alla cella in cui si incrociano la seconda colonna (xy=01) e la seconda riga (z=0) della mappa.
Quarta clausola
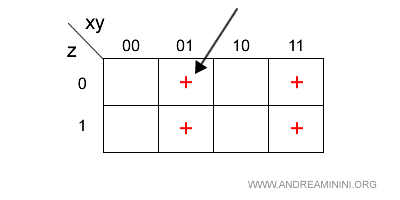
La quarta clausola dell'espressione è
$$ \overline{x}y\overline{z} $$
Equivale a xy = 01 e z=0.
Questa clausola corrisponde alla cella in cui si incrociano la seconda colonna (xy=01) e la prima riga (z=0) della mappa.
3] Raggruppare le celle confinanti in gruppi di 2, 4 o 8 elementi
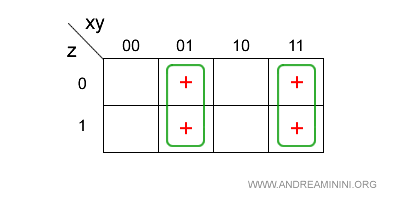
Una volta costruita la mappa di Karnaugh, posso raggruppare i simboli per potenze di 2.
Ogni gruppo deve essere composto da 2,4,8 simboli vicini tra loro.
I gruppi possono anche sovrapporsi parzialmente.
Nota. Le pareti della mappa di Karnaugh confinano con la parete opposta.
In questo caso, nella mappa ci sono due gruppi da 2.
3] Trasformare i gruppi in congiuzioni di letterali
Prendo ciascun gruppo e lo trasformo in una congiunzione, eliminando i letterali che assumono contemporaneamente i valori 0 e 1.
Primo gruppo
Nel primo gruppo xy assume il valore 01.
Elimino, invece, il letterale z perché ha sia il valore 0 che 1.
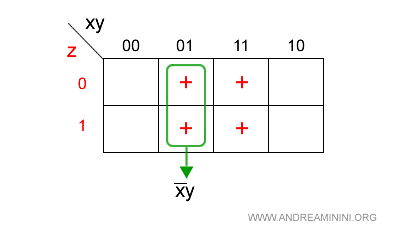
Il risultato finale è
$$ \overline{x}y $$
Secondo gruppo
Nel primo gruppo xy assume il valore 11.
Elimino, invece, il letterale z perché ha sia il valore 0 che 1.
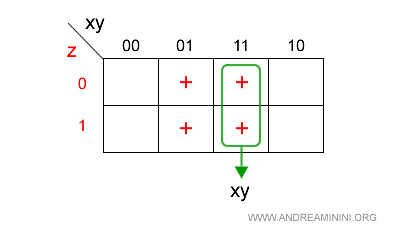
Il risultato finale è
$$ xy $$
4] Sommare le congiunzioni di letterali
Sommo tra loro le congiunzioni appena trovate e ottengo l'espressione booleana in forma ridotta della funzione booleana.
$$ \overline{x}y + xy $$
Il nuovo circuito logico è composto soltanto da due porte AND, una porta OR e una porta NOT.
Complessivamente, il circuito ha 4 porte.
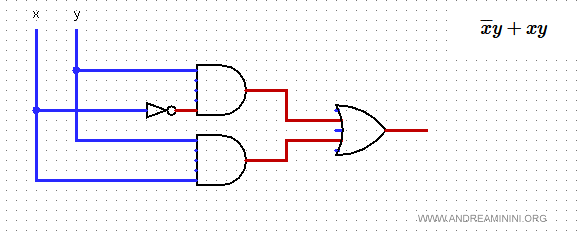
La tavola di verità dell'espressione è sempre la stessa.
Anche se non c'è più la lettera z, il valore 1 è abbinato alle stesse combinazioni x, y della precedente.
Nota. L'espressione è sicuramente migliore rispetto all'espressione iniziale. Tuttavia, non è ancora ottimale. Come si può vedere, nelle due clausole il letterale x appare sia in forma diretta che negata. $$ \overline{x}y + xy $$ Una semplice regola di semplificazione mi consente di eliminare la x in entrambe le clausole. L'espressione si riduce a $$ y+y $$ Un'altra legge dell'algebra booleana mi permette di ridurre ulteriormente l'espressione in $$ y $$ Perché la mappa di Karnaugh non l'ha trovata? Perché il risultato dipende anche dalla scelta dei gruppi di letterali e dall'ordine delle colonne nella mappa.
Come migliorare la mappa di Karnaugh
La riduzione di un'espressione booleana tramite la mappa di Karnaugh dipende dalla scelta dei gruppi e dall'ordine delle colonne.
Ad esempio, riprendo la precedente mappa scambiando la posizione della quarta e della terza colonna.
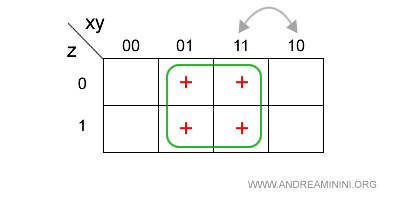
In questo modo creo un gruppo di quattro celle.
Il nuovo raggruppamento mi permette di semplificare ulteriormente il risultato finale.
Sia la z che la x appaiono con il valore zero e con il valore uno. Quindi, posso eliminarle.
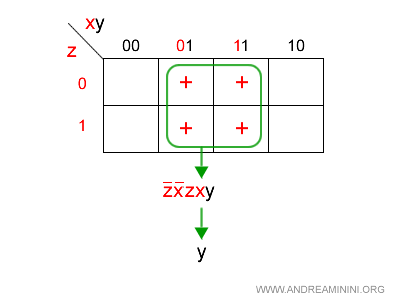
L'espressione finale è.
$$ y $$
Ovviamente l'espressione non può essere ulteriormente ridotta.
E così via
