La funzione booleana
Una funzione booleana di n variabili è una funzione con valori booleani sia nel dominio che nel codominio. $$ f:B^n \rightarrow B $$
Il dominio della funzione booleana può essere composto da una (n=1) o più variabili booleane (n>1).
$$ B^n = \underbrace{B \cdot B \cdot ... \cdot B }_n $$
Come costruire la tavola di verità della funzione booleana
Il valore di una funzione booleana è sempre un valore booleano.
Per calcolare il valore della funzione costruisco la tavola di verità, sostituendo i valori 0 e 1 a tutte le combinazioni possibili delle variabili booleane.
Esempio
Questa funzione booleana è composta dalla seguente espressione:
$$ f(x,y)= (x+y)x $$
Costruisco la tavola di verità della funzione.
Prima calcolo il valore della somma tra parentesi (x+y). Poi moltiplico il risultato per x.
$$ \begin{array}{cr|c} x & y & (x+y) & (x+y)x \\ \hline 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array} $$
La quarta colonna è il valore della funzione booleana.
A ogni combinazione possibile delle variabili booleane x,y è associato un valore f(x,y) specifico.
Essendo due variabili (n=2) ci sono 2n=22=4 combinazioni.
Nota. Questo semplice esempio dimostra che anche il valore della funzione è un valore booleano.
La differenza tra espressione e funzione booleana
Una funzione booleana ha una sola tavola di verità.
Tuttavia, la tavola di verità può essere ottenuta da diverse espressioni booleane.
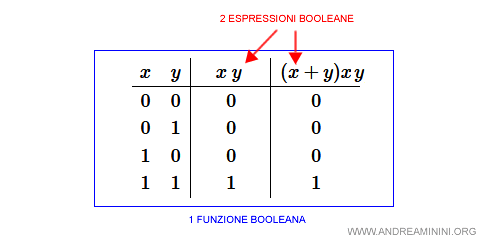
Quindi, per ogni espressione booleana esiste una sola funzione booleana ( tavola di verità ) ma non vale l'inverso.
Per ogni funzione booleana possono esistere diverse espressioni.
Nota. Costruire la tavola di verità da un'espressione booleana è molto semplice. Basta sostituire le combinazioni di zero e uno ai letterali. E' invece più complesso fare l'inverso, ossia costruire un'espressione booleana a partire da una tavola di verità. Nel prossimo paragrafo spiego come fare.
Come calcolare l'espressione booleana di una tavola di verità
Una tavola di verità ( funzione booleana ) può essere rappresentata da diverse espressioni booleane.
Una di queste è sicuramente un'espressione booleana in forma normale disgiuntiva (DNF).
Per ogni funzione booleana c'è sempre una forma normale disgiuntiva ed è unica.
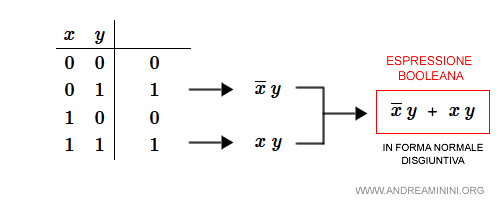
C'è un metodo abbastanza semplice per trovare l'espressione booleana a partire da una tavola di verità.
- Seleziono le righe della tavola di verità con i valore 1. Ignoro tutte le altre righe della tabella.
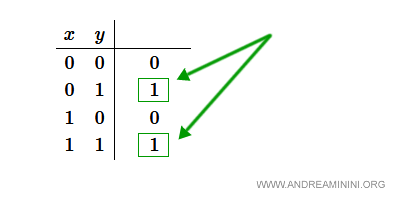
- Scrivo ogni riga selezionata come congiunzione di letterali. Nella congiunzione scrivo la variabile booleana (letterale) o la sua negazione a seconda se ha valore uno o zero nella tabella. Ottengo così una clausola composta dal prodotto dei letterali della riga tutti uguali a 1.
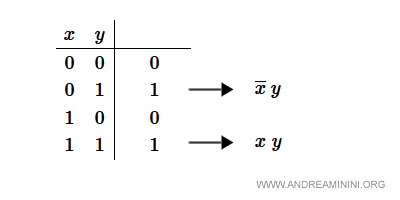
Nota. Una congiunzione xy assume il valore 1 per una sola combinazione di letterali. E' la combinazione in cui tutti i letterali hanno valore 1. Per questo motivo ho negato il letterale x nella prima riga selezionata della tabella. Nella prima riga il letterale x è 0. La sua negazione (x con trattino superiore) è 1. E così via.
- Sommo le congiunzioni tra loro. La somma delle clausole è l'espressione booleana in forma normale disgiuntiva (DNF). L'espressione in forma normale disgiuntiva è unica.
Le funzioni booleane uguali
Due funzioni booleane sono dette uguali se hanno la stessa tavola di verità.
Esempio
Le funzioni x(x+y) e (x+xy) hanno la stessa tavola di verità
$$ \begin{array}{cr|c} x & y & x(x+y) & (x+xy) \\ \hline 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array} $$
Le operazioni tra le funzioni booleane
Le principali operazioni tra le funzioni booleane sono le seguenti:
- Addizione $$ (f+g)(x,y) := f(x,y)+g(x,y) $$
- Moltiplicazione $$ (f \cdot g)(x,y) := f(x,y) \cdot g(x,y) $$
- Complemento $$ \overline{f}(x,y) := \overline{f(x,y)} $$
Le proprietà delle funzioni booleane
Le leggi booleane sono applicabili anche alle funzioni booleane.
Quindi, senza ripetersi valgono tutte le leggi già viste per le variabili booleane.

Nota. Le proprietà delle funzioni booleane sono le stesse dell'insiemistica e della logica delle proposizioni. I risultati sono equivalenti.
