Il principio di conservazione dell’energia
Il principio di conservazione dell'energia afferma che in un sistema isolato l’energia totale si conserva nel tempo.
In altre parole, l’energia non può essere creata né distrutta, ma solo trasformata da una forma all’altra. E' una delle leggi fondamentali della fisica.
Questo principio vale a prescindere dalla forma dell’energia (cinetica, potenziale, termica, chimica, ecc.) e anche quando passa da una forma all'altra.
- Energia cinetica ( $E_k $): legata al movimento di un corpo
- Energia potenziale ( $E_p $): legata alla posizione in un campo di forze
- Energia termica: legata all’agitazione delle particelle
- Energia chimica, elettrica, nucleare, luminosa...
Tuttavia, bisogna sempre ricordarsi la condizione fondamentale: il sistema deve essere un sistema isolato, cioè non deve scambiare energia (né materia) con l’ambiente esterno.
Se questa condizione non è soddisfatta, il bilancio energetico non è chiuso e l’energia può entrare o uscire dal sistema.
La legge di conservazione dell'energia
Nel caso di un sistema meccanico semplice (senza attriti), l’energia totale è sempre costante ed è data dalla somma:
$$ E = E_p + E_k = \text{costante} $$
Dove $ E_p $ è l'energia potenziale e $ E_k $ è l'energia cinetica
Nel caso generale, con più forme di energia:
$$ E_{\text{totale}} = E_{\text{cinetica}} + E_{\text{potenziale}} + E_{\text{termica}} + \dots = \text{costante} $$
La costanza dell’energia totale vale solo se tutte le forme coinvolte sono contabilizzate e non ci sono scambi con l’esterno, ossia se il sistema è isolato.
Esempi pratici
Esempio 1 - Caduta di un corpo
Considero una sfera lasciata cadere da un’altezza $h$ in assenza di attriti.
Inizialmente, quando la sfera la tengo ancora in mano, l'energia potenziale $E_p = mgh $, energia cinetica nulla.
Quando la faccio cadere la situazione cambia. Durante la caduta l'energia potenziale si riduce mentre l'energia cinetica aumenta.
Tuttavia, l’energia non scompare, ma si trasferisce da potenziale a cinetica.
$$ E_k(t) + E_p(t) = \text{costante} $$
Poco prima dell’impatto al suolo, l'energia potenziale è nulla $E_p \approx 0 $ e l'energia cinetica è massima $E_k = \frac{1}{2}mv^2$
Esempio pratico. Considero una sfera di massa $m = 0.5 \,\text{kg}$ lasciata cadere da un’altezza di $h = 2 \,\text{m}$, trascurando gli attriti. All’inizio, tutta l’energia è sotto forma di energia potenziale: $$ E_p = m g h = 0.5 \cdot 9.81 \cdot 2 \approx 9.81 \,\text{J} $$ mentre l’energia cinetica è nulla: $$E_k = 0 $$ L’energia totale iniziale del sistema risulta quindi: $$E_{\text{tot}} = 9.81 \,\text{J}$$ A metà del percorso $(h/2 = 1 \,\text{m})$, la situazione è bilanciata: metà dell’energia è ancora potenziale, metà si è già trasformata in cinetica. $$ E_p = m g h/2 = 0.5 \cdot 9.81 \cdot 1 = 4.905 \,\text{J} $$ $$ E_k = E_{\text{tot}} - E_p = 9.81 - 4.905 = 4.905 \,\text{J} $$ L'energia totale è sempre la stessa. $$ E_{\text{tot}} = E_p + E_k = 4.905 \,\text{J} + 4.905 \,\text{J} = 9.81 \,\text{J} $$ La velocità di caduta a metà percorso è: $$ E_k = \tfrac{1}{2} m v^2 \;\;\Rightarrow\;\; v = \sqrt{\tfrac{2 E_k}{m}} = \sqrt{\tfrac{2 \cdot 4.905}{0.5}} \approx 4.43 \,\text{m/s} $$ Poco prima dell’impatto al suolo, l’energia potenziale è ormai trascurabile: $$ E_p \approx 0 $$ mentre l’energia cinetica raggiunge il suo massimo valore: $$ E_k = E_{\text{tot}} = 9.81 \,\text{J} $$ La velocità con cui la sfera tocca terra è quindi: $$ v = \sqrt{\tfrac{2 E_k}{m}} = \sqrt{\tfrac{2 \cdot 9.81}{0.5}} = \sqrt{39.24} \approx 6.26 \,\text{m/s} $$ In conclusione, durante l’intera caduta, la somma tra energia potenziale e cinetica è rimasta invariata: $$ E_{\text{totale}} = E_p + E_k = 9.81 \,\text{J} = \text{costante} $$ L’energia non è mai andata perduta, ma si è semplicemente trasformata dall’una all’altra forma: da potenziale gravitazionale a cinetica.
Esempio 2 - Oscillazione di un pendolo
In un pendolo ideale (senza attrito) l'energia potenziale è massima quando la velocità è nulla, questo si verifica agli estremi, quando il pendolo cambia il verso del moto a fine corsa.
Al centro, invece, l'energia cinetica è massima, perché il pendolo raggiunge la sua velocità massima.
Anche in questo caso:
$$ E_k + E_p = \text{costante} $$
Nota. Se considerassi l’attrito con l’aria, l’energia meccanica non si conserverebbe, ma si trasformerebbe in calore. In ogni caso, la somma complessiva (meccanica + termica) si conserverebbe comunque. Il principio di conservazione dell'energia è soddisfatto.
Esempio 3 - Conversione energetica in una centrale
In una centrale termoelettrica l’energia chimica contenuta nel combustibile viene liberata attraverso una reazione di combustione.
La combustione produce gas ad alta temperatura che cedono energia termica a un fluido (di solito acqua), trasformandolo in vapore ad alta pressione.
Il vapore mette in rotazione una turbina, convertendo l’energia termica in energia meccanica rotazionale.
La turbina è collegata ad un alternatore, che trasforma l’energia meccanica in energia elettrica per induzione elettromagnetica.
L’energia totale si conserva in ogni passaggio, anche se cambia forma.
Nota. Parte dell’energia termica non viene convertita e si disperde sotto forma di calore. Tuttavia, in un sistema isolato, la somma dell’energia elettrica prodotta e di quella dispersa resta costante. Il principio di conservazione è rispettato.
La conservazione dell'energia nella fisica delle particelle
Il principio di conservazione dell'energia è universale e vale in tutte le interazioni fondamentali, che si tratti di decadimenti, collisioni o annichilazioni, l’energia totale prima e dopo l'interazione resta la stessa.
Ad esempio, nel decadimento beta un neutrone si trasforma in un protone, un elettrone e un antineutrino $ n \;\;\longrightarrow\;\; p + e^- + \bar{\nu}_e $ per via dell'interazione nucleare debole

In questo processo la massa a riposo non si conserva, perché la massa del neutrone iniziale è maggiore della somma delle masse del protone, dell'elettrone e dell'antineutrino.
Tuttavia, la differenza di massa non si perde, viene convertita in energia cinetica dei prodotti del decadimento ossia delle particelle emesse.
Il principio fondamentale è che ciò che rimane costante è l’energia totale, non la massa. Come mostrato dalla celebre relazione di Einstein:
$$ E = mc^2 $$
Quindi parte della massa a riposo può trasformarsi in energia cinetica o in radiazione.
In fisica il processo opposto è altrettanto possibile: l’energia disponibile può condensarsi in massa, ad esempio generando una coppia quark-antiquark.
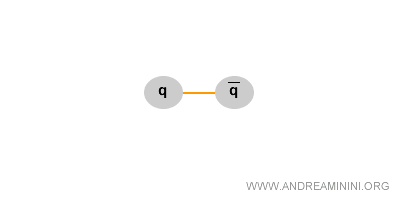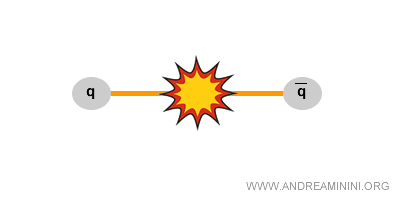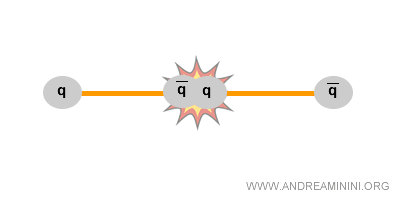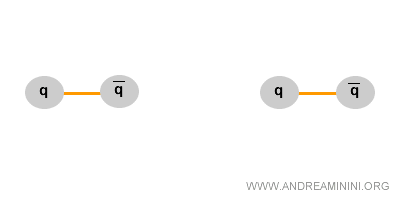
Per questo nelle reazioni nucleari e nei decadimenti di particelle la massa “sparisce” o “compare”, ma il bilancio energetico rimane invariato.
Nota. Oltre all’energia, nelle interazioni fondamentali si conservano anche altre quantità come la quantità di moto, le cariche (elettrica, di colore in QCD, numeri leptonici e barionici in certe condizioni), lo spin totale, ecc.
La conservazione dell'energia nell'Universo
Il principio di conservazione dell’energia è valido in tutti i contesti della fisica “locale”: dalla meccanica quantistica non relativistica fino alla teoria quantistica dei campi (QFT).
Tuttavia, in relatività generale la situazione cambia. In uno spazio-tempo curvo non sempre è possibile definire in modo univoco una “energia totale” dell’universo.
Questo perché il teorema di Noether lega la conservazione dell’energia all’invarianza rispetto a traslazioni temporali, ma nell’universo in espansione non esiste una simmetria temporale globale.
Un esempio emblematico è l’espansione cosmica: la densità di energia della radiazione diminuisce più rapidamente di quella della materia proprio perché lo spazio stesso si dilata. Non si tratta di un “trasferimento” di energia da un settore all’altro, ma di un effetto geometrico dello spazio-tempo in espansione.
Per questo motivo, molti cosmologi sostengono che parlare di “conservazione dell’energia totale dell’universo” sia privo di senso, mentre resta valido il principio di conservazione locale (cioè nei processi fisici descritti in un dato riferimento).
La questione, a livello globale, resta aperta ed è legata al problema ancora irrisolto di definire in modo coerente l’energia in relatività generale.
Fondamento teorico
La conservazione dell’energia è conseguenza diretta dell’invarianza delle leggi della fisica rispetto alle traslazioni nel tempo: le leggi non cambiano se ripetiamo un esperimento oggi o domani.
Il principio di conservazione dell’energia non è una legge empirica basata solo sull’osservazione.
È la conseguenza diretta di una simmetria fondamentale delle leggi fisiche.
In fisica, una simmetria non indica una figura geometrica, ma una trasformazione che lascia inalterato il comportamento di un sistema fisico.
Ad esempio, se un sistema si comporta allo stesso modo oggi, domani o tra un secolo, vuol dire che le leggi fisiche che lo descrivono non dipendono dal tempo ossia le leggi invarianti nel tempo.
Questa invarianza temporale implica che l’energia totale del sistema non cambia nel corso del tempo.
Questo legame tra simmetrie e quantità conservate è stato formalizzato in un teorema da Emmy Noether nel 1918. Secondo il teorema di Noether:
A ogni simmetria continua di un sistema fisico corrisponde una grandezza che si conserva nel tempo.
Nel caso della conservazione dell’energia, la simmetria è temporale: se le leggi non cambiano nel tempo, allora l’energia si conserva.
Il risultato vale sia nella meccanica classica, sia nelle teorie fisiche più avanzate come nella fisica quantistica.
E così via.
